
رگرسیون ریج چیست؟
دسترسی سریع
در این مقاله قصد داریم سوال متداولی که در مصاحبههای شغلی پرسیده میشود، یعنی "رگرسیون ریج چیست؟" را توضیح دهیم.
بسیاری از افراد که در زمینه تحلیل داده یا علم داده فعالیت میکنند، اغلب اوقات محدود به درک ابتدایی الگوریتمهای رگرسیون، به ویژه رگرسیون خطیهستند. تنها تعداد کمی از آنها با تکنیکهای منظمسازی (Regularization Techniques) مانند رگرسیون ریج و رگرسیون لسو (Lasso) آشنا هستند که به آنها کمک میکند تا مدلهای بهتری از دادهها بسازند. به عبارت دیگر، توانایی استفاده از تکنیکهای مختلف رگرسیون میتواند توانمندیهای تحلیل داده و علم داده را افزایش دهد.
این به ما کمی انگیزه میدهد تا توضیح دهیم که چگونه رگرسیون ریج در یادگیری ماشین کار میکند.
مفهوم رگرسیون ریج
رگرسیون ریج (Ridge Regression) روشی است برای ایجاد مدل سادهتر، زمانی که تعداد متغیرهای پیشبینی در مجموعه بیشتر از تعداد مشاهدات باشد، یا زمانی که یک مجموعه داده دارای چندین همبستگی (ارتباطات بین متغیرهای پیشبینی) باشد.
وقتی تعداد متغیرهای پیشبینی در یک مجموعه بیشتر از تعداد مشاهدات است، مشکلاتی ایجاد میشود. در این حالت، ممکن است مدل سعی کند تا با استفاده از همه این متغیرها، به دادهها بسیار خوب پاسخ دهد، اما این ممکن است باعث بیشبرازش شود و قابلیت تعمیم به دادههای جدید را از دست بدهد.
این نوع رگرسیون با اضافه کردن جملات جریمه L2 به تابع هدف، کمک میکند تا پارامترهای مدل کوچکتر شوند و تعداد متغیرهای مستقل مهم در مدل کاهش یابد. این کاهش تعداد متغیرها به وجود مدلی مناسب کمک میکند که قابلیت تعمیم به دادههای جدید را داشته باشد.
تفاوت بین روش تیخونوف و رگرسیون ریج
روش تیخونوف در اصل مشابه رگرسیون ریج است، با این تفاوت که تیخونوف یک مجموعه بزرگتر دارد. این روش میتواند راهحلهایی را تولید کند، حتی زمانی که مجموعه داده شما شامل تعداد زیادی نویز آماری (تغییر ناشی از دلایل غیر توضیحدهنده در یک نمونه) باشد.
وقتی مجموعه داده حاوی نویز آماری است، ممکن است رگرسیون سنتی با مشکل مواجه شود و نتایج نادقیقی را تولید کند. نویز آماری به تغییراتی در دادهها اشاره دارد که توسط مدل رگرسیون قابل توضیح نیستند و به تنهایی توضیح داده نمیشوند.
روش تیخونوف (یا تیخونوف-ملینینکوف) با اضافه کردن جملات جریمه L2 به تابع هدف، به مدل کمک میکند تا از تأثیر نویز آماری کاسته شود و راهحلهای پایدارتر و دقیقتری را ارائه دهد. این جملات جریمه به مدل اجازه میدهند تا پارامترهای کوچکتری داشته باشد و تأثیر نویز آماری را کاهش دهد.
یک مثال تخصصی برای رگرسیون ریج
رگرسیون ریج یکی از تکنیکهای رگرسیون منظمسازی است که برای کاهش بیشبرازش (overfitting) در مدلهای رگرسیونی به کار میرود. این روش به جای حداقلسازی مجموع مربعات خطاها (OLS)، مجموع مربعات خطاها و مجموع مربعات ضرایب رگرسیون را با هم حداقل میکند. به عبارتی دیگر، یک جریمه به اندازهی مجموع مربعات ضرایب به تابع هزینه اضافه میکند.
فرض کنید که دادههای زیر را داریم:

تابع هزینه در رگرسیون ریج
تابع هزینه در رگرسیون ریج به شکل زیر است:

مثال عملی
فرض کنید دادههای زیر را داریم:
| x1 | x2 | y |
|---|
| 1 | 2 | 4 |
| 2 | 3 | 5 |
| 3 | 4 | 6 |
| 4 | 5 |
7 |
ابتدا مدل رگرسیون خطی ساده بدون منظمسازی را برازش میدهیم:
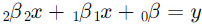
سپس مدل رگرسیون ریج را با اضافه کردن جریمه برازش میدهیم:
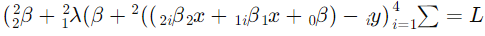
برای حل این مساله، میتوانیم از روشهای بهینهسازی عددی یا توابع موجود در کتابخانههای پایتون مانند scikit-learn استفاده کنیم. در اینجا یک پیادهسازی ساده با استفاده از scikit-learn آورده شده است:

نتیجه این کد ضرایب مدل و مقدار تقاطع را به شما نشان میدهد. با تغییر مقدار پارامتر جریمه alpha میتوانید تاثیر منظمسازی را مشاهده کنید.
تفاوت بین رگرسیون ریج و رگرسیون لسو
اختلاف اصلی بین رگرسیون لسو و رگرسیون ریج در اصطلاح جریمه (Penalty Term) است. تفاوتهای دیگر در جدول زیر آورده شده است.
| Ridge Regression | Lasso Regression |
|---|---|
| از تکنیک منظمسازی L2 استفاده میکند. | از تکنیک منظمسازی L1 استفاده میکند. |
| دلیل انجام این بهروزرسانی و تنظیم وزنها، وجود یک عبارت توان دوم اضافی در تابع خطا است. بدین معناست که تابع خطا در رگرسیون دارای یک عبارت توان دوم از وزنها است که بهصورت اضافی به تابع خطا اضافه میشود. | بهروزرسانی و تنظیم وزنها، بهدلیل وجود یک عبارت اضافی حاوی نرم L1 بردار وزنها در تابع خطا انجام میشود. |
| در هنگام بهینهسازی، این روش باعث کاهش اندازه کلی مقادیر وزنها میشود و به این ترتیب از بیشبرازش (overfitting) جلوگیری میکند. | این روش باعث کاهش وزن ویژگیهایی میشود که در یک نقطه خاص به صفر میرسند و در نتیجه ویژگیهایی که عاملی برای واریانس بالا و مشکلات بیشبرازش مدل هستند، بهطور مؤثر حذف میشوند. |
کاربرد رگرسیون ریج در پزشکی چیست؟
Ridge Regression در پزشکی بهعنوان یک روش تحلیل داده و مدلسازی آماری مورد استفاده قرار میگیرد. این روش میتواند در موارد مختلفی مفید باشد، از جمله:
• مدلسازی پیشبینی: رگرسیون ریج میتواند در پزشکی برای وظایف مدلسازی پیشبینی مانند پیشبینی نتایج بیماران یا پیشرفت بیماری استفاده شود. با یکپارچهسازی تنظیمات، به کاهش تأثیر چندخطی و بیشبرازش کمک میکند و منجر به پیشبینیهای دقیقتر میشود.
• انتخاب ویژگی: میتواند در شناسایی ویژگیها یا متغیرهای مرتبط در مجموعه دادههای پزشکی کمک کند. با اختصاص ضرایب کوچک و غیرصفر به متغیرهای کماطلاعات، ریج به ترتیب اولویتبندی پیشبینیکنندههای مهم و بهبود قابلیت تفسیر مدل کمک میکند.
• ژنومیک و ژنتیک: در مطالعات ژنومیک و ژنتیک، میتواند برای تحلیل دادههای بیان ژن، شناسایی نشانگرهای ژنتیکی مرتبط با بیماریها و پیشبینی خطر بیماری یا پاسخ به درمان استفاده شود. همچنین به مدیریت مجموعههای داده با ابعاد بالا با تعداد پیشبینندهای ممکن بالا کمک میکند و توانایی مدیریت ساختار همبستگی بین متغیرهای ژنتیکی را بهبود میبخشد.
• تصویربرداری پزشکی: رگرسیون ریدج میتواند در تجزیه و تحلیل دادههای تصویربرداری پزشکی مانند سونوگرافی یا اسکن CT مورد استفاده قرار گیرد. این روش در وظایفی مانند بازسازی تصویر، حذف نویز و استخراج ویژگیها کمک میکند. علاوه بر این، با ادغام منظمسازی، ریدج به کاهش نویز و بهبود کیفیت تصاویر پزشکی کمک میکند.
رگرسیون ریج در مقابل رگرسیون کمترین مربعات
رگرسیون کمترین مربعات (Least Squares) در مواقعی که تعداد متغیرهای پیشبینی بیشتر از تعداد دادهها باشد یا در مواجهه با متغیرهای مرتبط با یکدیگر مشکل داشته باشد، به مشکلاتی برمیخورد.
این روش تفاوتی بین متغیرهای "مهم" و "کماهمیت" در مدل ایجاد نمیکند، بنابراین همه آنها را در مدل در نظر میگیرد. این موجب بیشبرازش مدل و عدم توانایی در یافتن راهحلهای منحصر به فرد میشود. این نوع رگرسیون، همچنین با مشکلاتی در مواجهه با چندخطی در دادهها روبرو است.
ریج از تمام این مشکلات جلوگیری میکند. این بهدلیل این است که به تخمینگرهای بیطرف نیازی ندارد. در حالی که رگرسیون کمترین مربعات برآوردهای بیطرفی را تولید میکند، واریانسها ممکن است به گونهای بزرگ باشند که بهطور کامل نادرست باشند.
رگرسیون ریج مقدار کافی اریب را اضافه میکند تا برآوردها به عنوان تقریبهای قابل اعتمادی از مقادیر واقعی جمعیت باشند.
جمع شدگی و منظم سازی در مدل رگرسیون ریج چیست؟
روشهای انقباض (Shrinkage methods) یک تکنیک مدرن است که در آن از متغیرها بهصورت صریح استفاده نمیشود، بلکه مدلی را با تمام پارامترها متناسب میکنیم. این تکنیک از روشی استفاده میکند که تخمینهای ضرایب را محدود یا منظمسازی میکند، به عبارت دیگر، تخمینهای ضرایب را نسبت به تخمینهای کمترین مربعات به سمت صفر کاهش میدهد.
Shrinkage همچنین به عنوان regularization شناخته میشود و میتواند تأثیر کاهش واریانس داشته باشد و همچنین انتخاب متغیرها را انجام دهد.

تفسیرهای جایگزین برای رگرسیون ریج چیست؟
رگرسیون ریج میتواند بصورت بیزی تعبیر شود. اگر فرض کنیم که هر آمار پارامتری توقع مقدار صفر و واریانس داشته باشد، آنگاه رگرسیون ریج اغلب به عنوان راهحل بیزی نشان داده میشود. دیدگاه دیگری که توسط منتقدان ذکر شده است، نظریه "دادههای تقلبی" است.
اصولا نشان داده میشود که راهحل این رگرسیون با اضافه کردن سطرهای دانش به ماتریس اولیه دادهها بهدست میآید. این سطرها با استفاده از مقدار صفر برای متغیرهای وابسته و ریشه 'k' یا صفر برای متغیرهای مستقل ساخته میشوند.
برای هر متغیر تجربی یک سطر اضافه میشود. این ایده که دادههای تولیدی نتایج رگرسیون ریج را تولید میکنند، بسیاری از نگرانیها را به وجود آورده و منجر به افزایش جدال در استفاده و تفسیر آن شده است.
خلاصه کلام
رگرسیون ریج بهعنوان یک ابزار قدرتمند در تحلیل دادهها و مدلسازی آماری در مختلف حوزهها، از جمله پزشکی، بهکار میرود. این متد با استفاده از مفهوم منظمسازی و کاهش بیشبرازش، به ما امکان میدهد دقت و قدرت پیشبینی بالاتری در مدلهای آماری داشته باشیم. همچنین، تفاوتهای آن با رگرسیون لسو را نیز مشخص کردیم که میتواند در انتخاب مناسب برای مسائل مختلف کمک کند.
نظرات
هیچ نظری وجود ندارد.
افزودن نظر
مشاهده نقشه سایت
Copyright © 2017 - 2023 Khavarzadeh®. All rights reserved