رگرسیون چیست

تحلیل رگرسیون، یکی از مفاهیم کلیدی و حیاتی در آمار و یادگیری ماشین است که به تبیین و پیش‌بینی روابط بین متغیرها پرداخته و نقش بسیار مهمی در تصمیم‌گیری‌ها ایفا می‌کند. این تکنیک آماری پیچیده به ما امکان می‌دهد تا به سوالاتی مانند "چگونه متغیرها بر تغییرات یکدیگر تأثیر می‌گذارند؟" و "چگونه می‌توانیم مقادیر آینده را پیش‌بینی کنیم؟" پاسخ دهیم.
در این مقاله، با مفهوم رگرسیون آشنا می‌شویم و نشان می‌دهیم که چگونه می‌توانید از این تکنیک قدرتمند در تحلیل داده‌ها و پیش‌بینی‌های دقیق استفاده کنید.

رگرسیون چیست؟

رگرسیون (Regression) یکی از اصولی‌ترین روش‌های آماری است و در تحلیل داده‌های آماری به‌عنوان ابزار مهم مورد استفاده قرار می‌گیرد. با استفاده از رگرسیون، می‌توانیم بهترین مدلی که توصیف کننده رابطه بین متغیرهاست را پیدا کنیم. این مدل به ما این امکان را می‌دهد تا پیش‌بینی‌های دقیق‌تری در مورد متغیرهای وابسته براساس متغیرهای مستقل داشته باشیم. در کاربردهای وسیعی مانند علوم اجتماعی، علوم طبیعی، اقتصاد و مهندسی، رگرسیون به ما کمک می‌کند تا ارتباطات پیچیده بین متغیرها را بشناسیم و تفسیر کنیم.
همچنین فرآیندی که برای انجام تحلیل رگرسیون استفاده می‌شود، کمک می‌کند تا درک کنیم کدام عوامل مهم هستند، کدام عوامل می‌توانند نادیده گرفته شوند و چگونه این عوامل به یکدیگر تأثیر می‌گذارند.

تمایز رگرسیون از بازگشت به میانگین

رگرسیون به‌عنوان تکنیک آماری نباید با مفهوم رگرسیون به میانگین (بازگشت به میانگین mean reversion) اشتباه گرفته شود.
این مفهوم به این معناست که زمانی که یک متغیر به طور موقت از میانگین خود دور می‌شود، احتمالاً در مرحله بعد به سمت میانگین بازگشت می‌کند. به عنوان مثال، اگر یک گروه از افراد براساس یک متغیر مشخصی مانند قد مورد اندازه‌گیری قرار گیرند، افرادی که قد بالاتری نسبت به میانگین دارند، در میانگین کلی قرار گرفته و افرادی که قد پایین‌تری نسبت به میانگین دارند، همچنین به سمت میانگین حرکت می‌کنند. این ایده توسط عالم آماری فرانسوی فرانسوا گالتون مطرح شد و به عنوان رگرسیون به میانگین شناخته می‌شود.
بنابراین، درک این نکته مهم است که رگرسیون به‌عنوان تکنیک آماری و روش تحلیل داده‌ها استفاده می‌شود، در حالی که رگرسیون به میانگین به مفهوم بازگشت پدیده‌ها به میانگین است.

انواع تحلیل رگرسیون

برای انجام پیش‌بینی‌ها، رویکردهای متعدد تجزیه و تحلیل رگرسیون در دسترس هستند. انتخاب مناسب‌ترین روش آنالیز رگرسیون برای یک مسئله خاص به‌عوامل متعددی بستگی دارد. این عوامل شامل تعداد متغیرهای مستقل که در تحلیل استفاده می‌شود، شکلی که خط رگرسیون باید داشته باشد (مثلا خطی یا غیرخطی) و نوع متغیرهای وابسته که باید پیش‌بینی شوند. انتخاب درست این پارامترها می‌تواند به‌دقت و عملکرد مدل تاثیر بسزایی بگذارد، بنابراین انتخاب مناسب روش رگرسیون بسیار مهم است.

رگرسیون خطی (Linear regression):

رگرسیون خطی، ساده‌ترین و رایج‌ترین تحلیل پیش‌بینی است. تخمین‌های رگرسیون برای توصیف داده‌ها و توضیح رابطه استفاده می‌شوند.

مثال ساده از رگرسیون خطی:

فرض کنید می‌خواهیم تأثیر تعداد ساعت‌های مطالعه (X) را بر نمره امتحان (Y) بررسی کنیم. داده‌های زیر را در اختیار داریم:

تعداد ساعت‌های مطالعه (X)	نمره امتحان (Y)
1	2
2	4
3	5
4	4
5	5

حالا می‌خواهیم یک مدل رگرسیون خطی بسازیم تا رابطه بین X و Y را پیدا کنیم.

رگرسیون خطی به صورت 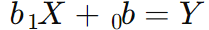است که در آن  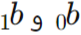به ترتیب عرض از مبدأ و شیب خط رگرسیون هستند.

ابتدا باید عرض از مبدأ و شیب خط رگرسیون را محاسبه کنیم.

فرمول‌های محاسبه به صورت زیر هستند.

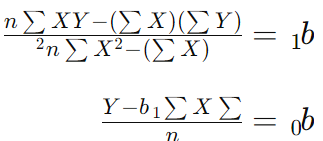
محاسبات:

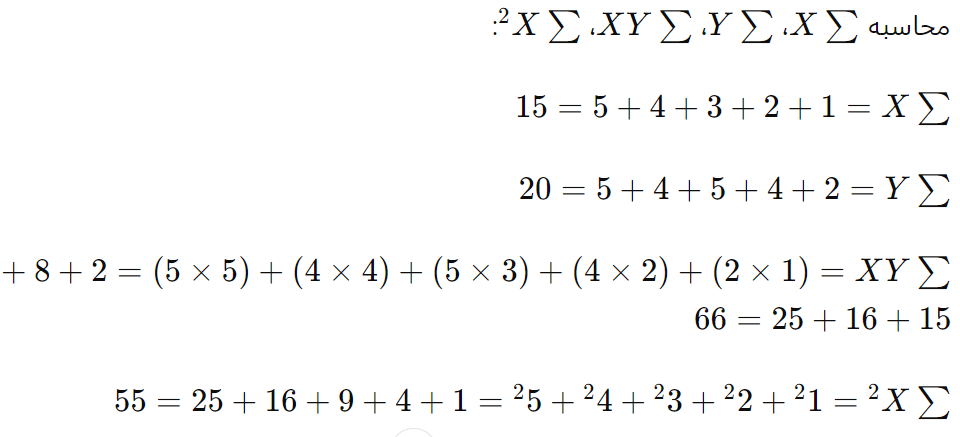
این معادله به ما می‌گوید که با هر یک ساعت افزایش در مطالعه، نمره امتحان به طور میانگین 0.6 واحد افزایش می‌یابد. همچنین وقتی هیچ مطالعه‌ای انجام نشده باشد (X=0)، نمره امتحان به طور میانگین 2.2 خواهد بود.

رگرسیون چندجمله ای (Polynomial regression):

روش تحلیل داده است که به ما اجازه می‌دهد رابطه بین متغیرهای وابسته و مستقل را با استفاده از یک چندجمله‌ای (یعنی یک عبارت ریاضی با توان‌های مختلف) مدل کنیم.

مثالی ساده برای رگرسیون چندجمله ای:

فرض کنید می‌خواهیم رابطه‌ی بین تعداد ساعات مطالعه (x) و نمره‌ی امتحان (y) را بررسی کنیم. داده‌های ما به صورت زیر است:

تعداد ساعات مطالعه (x)	نمره‌ی امتحان (y)
1	2
2	3
3	5
4	7
5	11

برای مدل‌سازی این داده‌ها با رگرسیون چندجمله‌ای، می‌توانیم از یک چندجمله‌ای درجه دوم (پارا‌بولا) استفاده کنیم. معادله‌ی چندجمله‌ای درجه دوم به صورت زیر است:

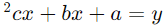
ما باید مقادیر a، b و c را به طوری پیدا کنیم که این معادله به بهترین نحو ممکن داده‌های ما را توضیح دهد. این کار معمولاً با استفاده از روش حداقل مربعات انجام می‌شود. فرض کنید با استفاده از این روش، مقادیر a، b و c به دست آمده است.

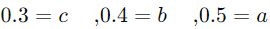
معادله‌ی چندجمله‌ای ما به صورت زیر خواهد بود:

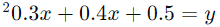
با استفاده از این معادله، می‌توانیم نمره‌ی امتحان را برای هر تعداد ساعات مطالعه‌ای پیش‌بینی کنیم. برای مثال، اگر فردی 3.5 ساعت مطالعه کند، پیش‌بینی نمره‌ی او عبارت است از:

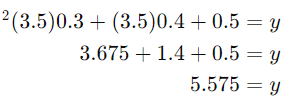
بنابراین، پیش‌بینی می‌شود که نمره‌ی امتحان این فرد 5.575 باشد.

رگرسیون لجستیک (Logistic regression):

یک روش تحلیل آماری است که برای پیش‌بینی نتایج دودویی یا احتمالات استفاده می‌شود. (مانند بله/خیر، درست/نادرست یا 0/1). برای اطلاعات بیشتر به مقاله آشنایی با رگرسیون لجستیک مراجعه کنید.

مثالی برای رگرسیون لجستیک:

فرض کنید داده‌های زیر را داریم که نشان‌دهنده تعداد ساعات مطالعه (x) و نتیجه امتحان (y) است. در این مثال، y می‌تواند دو مقدار 0 (رد شده) یا 1 (قبول شده) را داشته باشد:

تعداد ساعات مطالعه (x)	نتیجه امتحان (y)
1	0
2	0
3	0
4	1
5	1
6	1
7	1
8	1

در رگرسیون لجستیک، ما به دنبال یافتن رابطه‌ای به شکل زیر هستیم:

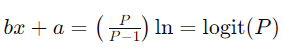
که در آن P احتمال وقوع نتیجه‌ی 1 (قبول شدن) است. این معادله می‌تواند به صورت زیر بازنویسی شود تا احتمال P را مستقیم محاسبه کنیم:

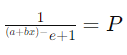
فرض کنید با استفاده از روش حداکثر درست‌نمایی، مقادیر a و b را به دست آورده‌ایم:

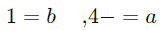
معادله‌ی ما به صورت زیر خواهد بود:

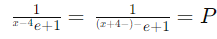
حال، می‌توانیم از این معادله برای پیش‌بینی احتمال قبول شدن یک دانشجو بر اساس تعداد ساعات مطالعه استفاده کنیم. به عنوان مثال، اگر یک دانشجو 6 ساعت مطالعه کرده باشد، احتمال قبول شدن او به شکل زیر است.

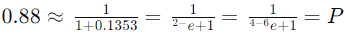
بنابراین، احتمال قبول شدن این دانشجو 88% است.

رگرسیون لجستیک می‌تواند به خوبی برای مدل‌سازی داده‌هایی که نتیجه آنها دودویی است، مانند پیش‌بینی بیماری، موفقیت در امتحان، یا هر پدیده دیگری که دو حالت ممکن دارد، استفاده شود.

 رگرسیون ریج (Ridge regression):

رگرسیون ریچ نوع مدل رگرسیون خطی است که در تجزیه و تحلیل چند متغیره، وجود همبستگی چندگانه (multicollinearity) را بررسی می‌کند. هدف آن کاهش مجموع خطاهای مربعی بین مقادیر واقعی و پیش‌بینی شده است، با اضافه کردن یک جریمه که ضرایب را کاهش داده و به سمت صفر نزدیک می‌کند.

مثالی ساده درباره رگرسیون ریج:

فرض کنید ما داده‌های زیر را داریم که شامل تعداد ساعات مطالعه (X) و نمره امتحان (Y) است:

تعداد ساعات مطالعه (X)	نمره امتحان (Y)
1	2
2	3
3	5
4	7
5	11
6	13
7	17
8	19

در رگرسیون خطی ساده، معادله رگرسیون به صورت زیر است:

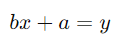
اما در رگرسیون ریج، ما یک ترم پنالتی به شکل 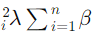 به تابع هزینه اضافه می‌کنیم، که  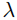یک هایپرپارامتر است که تعیین می‌کند میزان پنالتی چقدر باشد. بنابراین، تابع هزینه در رگرسیون ریج به صورت زیر است:

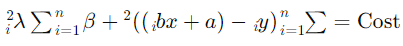
حال فرض کنید که پس از محاسبه، مقادیر a و b به صورت زیر به دست آمده‌اند (با یک مقدار فرضی ):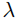

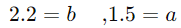
معادله رگرسیون ریج ما به صورت زیر خواهد بود:

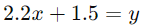
اکنون می‌توانیم از این معادله برای پیش‌بینی نمره امتحان بر اساس تعداد ساعات مطالعه استفاده کنیم. به عنوان مثال، اگر یک دانشجو 6 ساعت مطالعه کرده باشد، پیش‌بینی نمره او چنین است که:

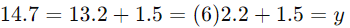
بنابراین، پیش‌بینی می‌شود که نمره امتحان این دانشجو 14.7 باشد.

رگرسیون لسو (Lasso regression):

روش تحلیل داده در زمینه یادگیری ماشین و آمار است که به ما امکان می‌دهد از طریق انتخاب وزن‌دهی به متغیرها، مدل رگرسیون را ساده‌تر کنیم و تأثیر متغیرهای مهم را افزایش دهیم. در این روش، از یک شاخص به نام "جریمه لسو" استفاده می‌شود که به ما اجازه می‌دهد متغیرهای غیرضروری را با وزن‌های صفر حذف کنیم.

مثالی درباره رگرسیون لسو:

فرض کنید داده‌های زیر را داریم که شامل تعداد ساعات مطالعه (X) و نمره امتحان (Y) است:

تعداد ساعات مطالعه (X)	نمره امتحان (Y)
1	2
2	3
3	5
4	7
5	11
6	13
7	17
8	19

اما در رگرسیون لسو، ما یک ترم پنالتی به شکل 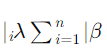 به تابع هزینه اضافه می‌کنیم، که  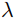یک هایپرپارامتر است.

بنابراین، تابع هزینه در رگرسیون لسو به صورت زیر است:

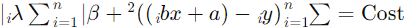
حال فرض کنید که پس از محاسبه، مقادیر aaa و bbb به صورت زیر به دست آمده‌اند:

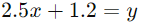
معادله رگرسیون لسو ما به صورت زیر خواهد بود:

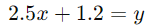
اکنون می‌توانیم از این معادله برای پیش‌بینی نمره امتحان بر اساس تعداد ساعات مطالعه استفاده کنیم. به عنوان مثال، اگر یک دانشجو 6 ساعت مطالعه کرده باشد، پیش‌بینی نمره او به صورت زیر خواهد بود:

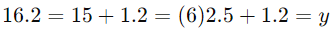
بنابراین، پیش‌بینی می‌شود که نمره امتحان این دانشجو 16.2 باشد.

رگرسیون الاستیک نت (Elastic Net Regression):

از ترکیب دو تکنیک رگرسیون لسو و رگرسیون ریج برای مدل‌سازی استفاده می‌کند. این روش این امکان را می‌دهد که هم فواید مهم هر دو تکنیک را بهره‌بریم و هم از مشکلات آن‌ها کاسته شود.

مثالی درباره رگرسیون الاستیک نت:

X1	X2	Y
1	2	3
2	3	5
3	4	7
4	5	9
5	6	11
6	7	13
7	8	15
8	9	17

در رگرسیون خطی ساده، معادله رگرسیون به صورت زیر است:

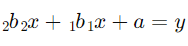
اما در رگرسیون الاستیک نت، تابع هزینه به صورت زیر است:

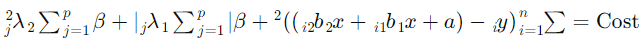
که 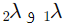 هایپرپارامترهایی هستند که تعیین می‌کنند میزان پنالتی چقدر باشد. این دو ترم پنالتی به ترتیب برای مقادیر مطلق ضرایب (Lasso) و مربعات ضرایب (Ridge) استفاده می‌شوند.

فرض کنید پس از محاسبه، مقادیر 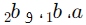 به صورت زیر به دست آمده‌اند.

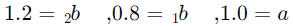
معادله رگرسیون الاستیک نت ما به صورت زیر خواهد بود:

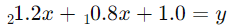
اکنون می‌توانیم از این معادله برای پیش‌بینی مقادیر Y بر اساس مقادیر X1 و X2 استفاده کنیم. به عنوان مثال، اگر 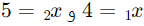 باشد، پیش‌بینی y به صورت زیر خواهد بود:

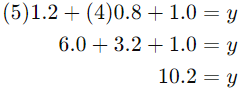
بنابراین، پیش‌بینی می‌شود که مقدار Y برابر با 10.2 باشد. رگرسیون الاستیک نت به ویژه زمانی مفید است که داده‌ها دارای تعداد زیادی ویژگی هستند و برخی از این ویژگی‌ها کمتر اهمیت دارند.

رگرسیون ماشین بردار پشتیبان (Support Vector Regression):

روش تحلیل داده در زمینه یادگیری ماشین است که برای مدل‌سازی و پیش‌بینی مقادیر عددی بر اساس داده‌های ورودی استفاده می‌شود. در این روش، ما از مفهوم بردارهای پشتیبان (Support Vectors) برای تشکیل یک حاشیه (Margin) حول نقاط داده استفاده می‌کنیم.

مثالی درباره رگرسیون ماشین بردار پشتیبان:

فرض کنید داده‌های زیر را داریم که شامل ویژگی X و نتیجه Y است:

X	Y
1	2
2	3
3	5
4	7
5	11
6	13
7	17
8	19

مراحل انجام ماشین بردار پشتیبان با استفاده از SVR:

1. پیش‌پردازش داده‌ها: ابتدا داده‌ها را نرمال‌سازی یا استانداردسازی می‌کنیم.
2. انتخاب مدل و کرنل: مدل SVR را با انتخاب نوع کرنل (مثل کرنل خطی، چندجمله‌ای یا RBF) مشخص می‌کنیم.
3. آموزش مدل: مدل را با استفاده از داده‌های آموزش تمرین می‌دهیم.
4. پیش‌بینی: مدل آموزش‌دیده را برای پیش‌بینی مقادیر جدید استفاده می‌کنیم.

پیاده‌سازی ماشین بردار پشتیبان با استفاده از پایتون و کتابخانه scikit-learn

در اینجا کدی برای پیاده‌سازی SVR با استفاده از کتابخانه scikit-learn آورده شده است:

توضیحات کدهای تصویر بالا

• استانداردسازی داده‌ها: از StandardScaler برای استانداردسازی داده‌ها استفاده می‌شود تا مدل به درستی آموزش ببیند.
• ایجاد مدل SVR: یک مدل SVR با کرنل RBF (Radial Basis Function) ایجاد می‌شود. پارامترهای C, gamma و epsilon تنظیم می‌شوند تا مدل بهترین عملکرد را داشته باشد.
• آموزش مدل: مدل با استفاده از داده‌های استانداردسازی شده آموزش داده می‌شود.
• پیش‌بینی: مدل آموزش‌دیده برای پیش‌بینی مقادیر Y استفاده می‌شود.
• نمایش نتایج: نمودار داده‌های واقعی و پیش‌بینی‌شده رسم می‌شود.

رگرسیون جنگل تصادفی: RANDOM FOREST regression:

روش پیش‌بینی مقادیر عددی در یادگیری ماشین است. در این روش، از یک مجموعه از درخت‌های تصادفی برای ایجاد مدل استفاده می‌کنیم. هر درخت در این مجموعه به صورت تصادفی با داده‌ها و ویژگی‌ها آموزش داده می‌شود و سپس می‌تواند پیش‌بینی‌های خود را ارائه دهد.

مثالی درباره رگرسیون جنگل تصادفی:

فرض کنید داده‌های زیر را داریم که شامل دو ویژگی (متغیر مستقل) X1 و X2 و یک نتیجه (متغیر وابسته) Y است:

X1	X2	Y
1	2	3
2	3	5
3	4	7
4	5	9
5	6	11
6	7	13
7	8	15
8	9	17

مراحل انجام رگرسیون با استفاده از جنگل تصادفی:

1. پیش‌پردازش داده‌ها: ابتدا داده‌ها را به فرمت مناسب برای مدل تبدیل می‌کنیم.
2. ایجاد مدل جنگل تصادفی: مدل جنگل تصادفی را با تعداد مشخصی از درختان تصمیم‌گیری ایجاد می‌کنیم.
3. آموزش مدل: مدل را با استفاده از داده‌های آموزشی تمرین می‌دهیم.
4. پیش‌بینی: مدل آموزش‌دیده را برای پیش‌بینی مقادیر جدید استفاده می‌کنیم.

پیاده‌سازی با استفاده از پایتون و کتابخانه scikit-learn

در اینجا کدی برای پیاده‌سازی رگرسیون جنگل تصادفی با استفاده از کتابخانه scikit-learn آورده شده است:

توضیحات کد تصویر بالا:

• ایجاد مدل جنگل تصادفی: یک مدل جنگل تصادفی با 100 درخت تصمیم‌گیری ایجاد می‌شود. پارامتر random_state برای اطمینان از تکرارپذیری نتایج استفاده می‌شود.
• آموزش مدل: مدل با استفاده از داده‌ها آموزش داده می‌شود.
• پیش‌بینی: مدل آموزش‌دیده برای پیش‌بینی مقادیر Y استفاده می‌شود.
• نمایش نتایج: نمودار داده‌های واقعی و پیش‌بینی‌شده رسم می‌شود.

 

افراد هنگام کار با تحلیل رگرسیون چه اشتباهاتی مرتکب می‌شوند؟

هنگام کار با تحلیل رگرسیون، مهم است مسئله مورد نظر را به درستی درک کنیم. اگر مسئله مطرح شده درباره پیش‌بینی باشد، احتمالاً باید از رگرسیون خطی استفاده کنیم. اگر مسئله مطرح شده درباره طبقه‌بندی دودویی باشد، باید از رگرسیون لجستیک استفاده کنیم. به همین ترتیب، بسته به مسئله مطرح شده، ما باید تمام مدل‌های رگرسیون خود را ارزیابی کنیم.

رگرسیون و اقتصادسنجی

اقتصادسنجی (Econometrics) مجموعه‌ای از تکنیک‌های آماری است که برای تحلیل داده‌ها در حوزه مالی و اقتصاد استفاده می‌شود. یکی از کاربردهای اقتصادسنجی، مطالعه تأثیر درآمد با استفاده از داده‌های قابل مشاهده است. به‌عنوان مثال، یک اقتصاددان ممکن است فرض بر این بگذارد که با افزایش درآمد فرد، مصرف او نیز افزایش خواهد یافت.
اگر داده‌ها نشان دهند که چنین ارتباطی وجود دارد، می‌توان تحلیل رگرسیونی انجام داد تا قدرت ارتباط بین درآمد و مصرف و همچنین اینکه آیا این ارتباط به‌صورت آماری معنادار است یا خیر را درک کنیم؛ به‌عبارت دیگر، آیا به نظر می‌رسد این ارتباط تنها به دلیل اتفاقات تصادفی است یا خیر.
توجه داشته باشید که می‌توانید در تحلیل خود از چندین متغیر توضیحی استفاده کنید، برای مثال، تغییرات تولید ناخالص داخلی (GDP) و تورم به‌علاوه نرخ بیکاری برای توضیح قیمت‌های بورس. وقتی از بیش از یک متغیر توضیحی استفاده می‌شود، به آن رگرسیون خطی چندگانه گفته می‌شود. این ابزار بیشترین استفاده را در اقتصادسنجی دارد.

گاهی اوقات اقتصادسنجی به‌خاطر وابستگی زیاد به تفسیر نتایج رگرسیون بدون ارتباط آن با تئوری اقتصادی یا جستجوی مکانیسم‌های علیتی مورد انتقاد قرار می‌گیرد. این مهم است که یافته‌های به‌دست آمده از داده‌ها توسط یک تئوری به‌طور مناسب توضیح داده شوند، حتی اگر این به‌معنای ایجاد یک تئوری جدید از فرآیندهای زیربنایی باشد. به عبارت دیگر، باید توجیهی نظری برای رابطه مشاهده شده در داده‌ها وجود داشته باشد.

کاربردهای تحلیل رگرسیون

 

شرکت‌های دارویی

شرکت‌های دارویی از تحلیل رگرسیون برای تجزیه و تحلیل داده‌های کمی پایداری در طول دوره تست مجدد یا برآورد عمر مفید استفاده می‌کنند. در این روش، طبیعت رابطه بین یک ویژگی و زمان را مشخص می‌کنیم. با استفاده از داده‌های تجزیه و تحلیل شده، تعیین می‌شود که آیا داده‌ها برای تحلیل رگرسیون خطی یا غیرخطی باید تبدیل شوند.
در اینجا یک مثال را برای روشن‌تر شدن مفهوم توضیح می‌دهیم:
فرض کنید شرکت دارویی یک داروی خاص تولید می‌کند و می‌خواهد عمر مفید این دارو را تخمین بزند. برای انجام این کار، شرکت به‌مدت مدیدی داده‌هایی جمع‌آوری می‌کند که مربوط به پایداری دارو در طول زمان است. این داده‌ها شامل اطلاعاتی مانند دما، رطوبت، نور، ویژگی‌های شیمیایی و زمان ذخیره‌سازی دارو می‌شوند.
حالا با استفاده از تحلیل رگرسیون، شرکت دارویی می‌تواند بررسی کند که چگونه این عوامل مختلف تاثیری بر پایداری دارو دارند. به‌عبارت دقیق‌تر، با تحلیل رگرسیون می‌توان مدلی ریاضی ایجاد کرد که نشان دهد چگونه تغییرات در دما، رطوبت، و دیگر ویژگی‌ها در طول زمان باعث تغییر در کیفیت و پایداری دارو می‌شوند.
شرکت با استفاده از تحلیل رگرسیون می‌تواند بهبود در کنترل کیفیت محصولات خود داشته باشد و به افزایش اعتماد مصرف‌کنندگان به داروهای تولیدی خود بیشتر کمک کند.

مالی

در علم مالی، رگرسیون خطی ساده به عنوان یک ابزار تحلیلی معمولی برای بررسی روابط بین متغیرها در تحلیل مالی و پیش‌بینی موردهای مالی استفاده می‌شود. این تکنیک به صورت مخصوص در مدل CAPM نیز مورد استفاده قرار می‌گیرد تا رابطه بین ریسک (خطر) سرمایه‌گذاری در بازار مالی و بازده مورد انتظار ارائه دهد. این اطلاعات اهمیت زیادی در تصمیم‌گیری‌های مالی دارد و به کمک متخصصان مالی در تحلیل و ارزیابی سرمایه‌گذاری‌ها می‌آید.
کاربرد رگرسیون در حوزه مالی با مثال
یکی از مثال‌های کاربردی این تکنیک در مالی، استفاده از رگرسیون برای تخمین بازدهی یک سهام به‌عنوان وابسته به‌عواملی مانند نرخ سود بانک مرکزی، نرخ تورم، و نرخ رشد اقتصادی است.
برای مثال، یک محل تجاری (فروشگاه‌ها، مغازه‌ها، ادارات مالی، شرکت‌ها، ادارات، انبارها، کارخانه‌ها و سایر واحدهای مشابه) که در حوزه سرمایه‌گذاری فعالیت می‌کند ممکن است بخواهد بازدهی سهام خود را در آینده پیش‌بینی کند تا تصمیم‌های سرمایه‌گذاری بهتری بگیرد. در اینجا، او می‌تواند از تحلیل رگرسیون استفاده کند تا بررسی کند که چگونه تغییرات در نرخ سود بانک مرکزی، نرخ تورم و نرخ رشد اقتصادی تأثیری بر بازدهی سهام دارند. 
این تحلیل می‌تواند به او کمک کند تا بهترین تصمیم‌های مالی برای سرمایه‌گذاری در سهام خود بگیرد و ریسک و بازده سرمایه‌گذاری‌هایش را بهبود بخشد. این نشان می‌دهد که رگرسیون به‌عنوان یک ابزار مهم در تصمیم‌گیری‌های مالی و سرمایه‌گذاری در بازار سرمایه دارای کاربردهای متعددی است.

رگرسیون در علم داده و تجزیه و تحلیل داده

روش رگرسیون در پیش‌بینی، همانطور که نامش نشان می‌دهد، برای پیش‌بینی و یافتن رابطه علتی بین متغیرها استفاده می‌شود. از نگاه کسب و کار، روش رگرسیون برای افرادی که با داده‌ها کار می‌کنند، در موارد زیر می‌تواند مفید باشد:
•    پیش‌بینی فروش در دوره‌های نزدیک و بلندمدت
•    درک تقاضا و عرضه.
•    درک میزان موجودی کالاها
•    بررسی و درک اینکه چگونه متغیرها بر همه این عوامل تأثیر می‌گذارند.
همچنین، کسب‌وکارها می‌توانند از روش‌های رگرسیون برای درک موارد زیر استفاده کنند:
•    چرا تماس‌های خدمات مشتری در ماه‌های گذشته کاهش یافته‌ است؟
•    فروش در شش ماه آینده چگونه خواهد بود؟
•    کدام روش "تبلیغاتی" را انتخاب کنیم؟
•    آیا باید کسب و کار را گسترش دهیم یا محصول جدیدی را ایجاد و بازاریابی کنیم؟
در اینجا روش رگرسیون به‌عنوان یک ابزار تحلیلی قوی در علم داده و تجزیه و تحلیل داده معرفی شده است که به ما کمک می‌کند تا رابطه بین متغیرها را درک کرده، پیش‌بینی‌هایی برای آینده بسازیم و از داده‌ها در زمینه‌های مختلف و کاربردهای گوناگون بهره‌برداری کنیم.

خلاصه کلام

رگرسیون یکی از ابزارهای حیاتی تحلیل داده‌ها است که درزمینه‌های مختلف به‌کار می‌رود. این تکنیک این امکان را می‌دهد تا روابط پیچیده داده‌ها را تفسیر کرده و پیش‌بینی‌های دقیق‌تری انجام دهیم. از اقتصاد و مالی تا علوم پزشکی و مهندسی، رگرسیون ابزاری توانمند برای تحلیل داده‌ها و ایجاد مدل‌های پیش‌بینی است.