تجزیه و تحلیل واریانس (ANOVA)

واریانس چیست؟

تجزیه و تحلیل واریانس (ANOVA) یک روش آماری است که برای مقایسه میانگین‌های دو یا چند گروه به کار می‌رود. این روش کمک می‌کند تا مشخص شود آیا تفاوت‌های معنی‌داری بین میانگین‌های گروه‌ها وجود دارد یا خیر.

تجزیه و تحلیل واریانسANOVA

در این مبحث قبل از توضیح آزمون تحلیل واریانس یک راهه لازم است به طور اختصار کاربرد آزمون t گروه های مستقل را که در قسمت آزمون های t توضیح داده شده است، دوباره مرور کنیم. همان طوری که قبلا گفته شد زمانی که دو جامعه مستقل از نظر یک متغییر که با مقیاس نسبتی یا فاصله ای اندازه اگیری شده اند، با هم مقایسه می شوند، آزمون t برای گروه های مستقل مناسب است. به عنوان مثال درمانگری، دو روش درمانی متفاوت را جهت کاهش اضطراب بیماران خود در دو گروه جداگانه به کار گرفته است. این درمانگر، پس از طی دوره درمان با استفاده از مقیاس اضطراب زانگ، میزان اضطراب را در هر دو گروه اندازه گیری می کند اضطراب در اینجا یک متغییر فاصله ای وابسته است. وی پس از محاسبه میانگین اضطراب در هر گروه به طور جداگانه، برای آزمون معنی دار بودن فرض تفاوت میانگین اضطراب آن دو گروه از آزمون t استفاده می کند. این پژوهشگر جهت آزمون فرض، سطح معنی داری را ۰/۰۵ = a در نظر می گیرد. به عبارت دیگر احتمال این که فرض صفر درست را رد کند ۰/۰۵ خواهد بود. در نظر بگیرید که پس از مدتی درمانگر محقق ما با یک روش جدید درمانی برای بیماران مضطرب آشنا می شود و تصمیم می گیرد که تاثیر سه روش درمانی را در کاهش اضطراب بیماران مقایسه کند. پس از طی دوره درمان با سه روش درمانی بر روی سه گروه، با استفاده از مقیاس اضطراب زانگ، سه میانگین اضطراب برای سه گروه را محاسبه می کند. اکنون این پژوهشگر با فرض متفاوتی روبرو است و آن، فرض عدم تفاوت معنی دار بین سه میانگین از سه جامعه مستقل است. وی برای آزمون فرض صفر خود از چه آزمون آماری استفاده خواهد کرد؟ آیا استفاده از آزمون t بدین ترتیب که چند مقایسه و چند آزمون t اجرا شود، امکان پذیر است؟ یعنی بار اول، میانگین گروه اول ( روش درمانی ۱ ) با میانگین گروه دوم ( روش درمانی ۲ ) و بار دوم، میانگین گروه اول ( روش درمانی ۲ ) با میانگین گروه سوم ( روش درمانی ۳ ) و بار سوم، میانگین گروه دوم ( روش درمانی ۲ ) با میانگین گروه سوم ( روش درمانی ۳ ) مقایسه شود. ملاحظه می کنید که برای مقایسه سه گروه، سه آزمون t خواهیم داشت که حجم کار ما را زیاد خواهد کرد. علاوه بر آن زیاد شدن آزمون های t موجب افزایش احتمال خطای نوع اول خواهد بود. فرض کنید سطح معنی دار بودن را برای هر یک از این آزمون ها ۰/۰۵ = a در نظر گرفته ایم بنابراین احتمال این که فرض صفر ( نبودن تفاوت بین دو میانگین ) را رد کنیم ۵ درصد و احتمال رد نکردن آن ۹۵ درصد خواهد بود. بنابراین احتمال رد نکردن فرض صفر در سه آزمون t، (۰/۹۵)^۳=۰/۸۶ خواهد بود. به عبارت دیگر ۰/۹۵ را به تعداد آزمون های t به توان می رسانیم. در نتیجه احتمال رد کردن حداقل یک فرض صفر ( عدم تفاوت معنی دار ) برابر با a – ۱ یعنی ۰/۱۴ = ( ۰/۸۶ – ۱ ) خواهد بود. بر این اساس است که احتمال ارتکاب خطای نوع اول با افزایش تعداد میانگین ها و زیاد شدن آزمون های t افزایش می یابد به طوری که در این جا که سه آزمون t وجود دارد سطح معنی دار ۰/۰۵ به ۰/۱۴ می رسد. حال اگر به جای مقایسه سه میانگین از سه جامعه مستقل، هدف پژوهشگر مقایسه چهار میانگین باشد، چهار مقایسه زوجی خواهیم داشت و بدین ترتیب باید شش آزمون t محاسبه شود که در این صورت، احتمال این که فرض صفر را رد نکنیم برابر 〖(۰/۹۵)〗^۶=۰/۷۴ خواهد بود و احتمال رد کردن دست کم یک فرض برابر با ۰/۲۶ = ( ۰/۷۴ – ۱ ) به دست خواهد آمد در واقع در این جا با اضافه شدن میانگین ها یا جامعه های مورد مقایسه و به کارگیری آزمون های t بیشتر برای آزمون تفاوت معنی دار بین چندین میانگین، احتمال ارتکاب خطای نوع اول بیشتر می شود، به طوری که به کارگیری شش آزمون t برای مقایسه چهار میانگین، احتمال ارتکاب خطای نوع اول را به ۰/۲۶می رساند. همان طوری که خود نیز محاسبه کردید برای مقایسه پنج میانگین از پنج جامعه مستقل با متغییر مقیاس فاصله ای، ۱۰ آزمون t لازم است که در آزمون t، یک مقایسه دوتایی انجام گیرد و احتمال تفاوت معنی دار میانگین ها که همان احتمال ارتکاب خطای نوع اول نیز است، در این آزمون برابر با ۰/۴۰ می شود. زیرا احتمال رد نکردن فرض صفر، برابر با 〖(۰/۹۵)〗^۱۰=۰/۶۰ بوده و در نتیجه احتمال رد کردن دست کم یک فرض صفر برابر با ۰/۴۰ = ( ۰/۶۰ – ۱ ) خواهد بود. بدین ترتیب به علت زیاد شدن حجم کار و افزایش احتمال ارتکاب خطای نوع اول، برای آزمون معنی داری تفاوت بین چند میانگین، لازم است از روش دیگری استفاده شود. یکی از معروف ترین روش های آماری که در این گونه مسائل پژوهشی کاربرد فراوان دارد روش تحلیل واریانس یا ANOVA مخفف اصطلاح Analysis OF Variance است. روش تجزیه و تحلیل واریانس در سال ۱۹۲۰ توسط فیشر توسعه یافت. روش تجزیه و تحلیل واریانس انواع مختلفی دارد که ساده ترین نوع آن تجزیه و تحلیل واریانس یک طرفه است که در این قسمت چگونگی محاسبه آن را در مراحل مختلف توضیح خواهیم داد ولی قبل از این توضیحات لازم است که با  <تحلیل واریانس و کاربردهای آن> بیشتر آشنا شویم.

مفهوم تجزیه و تحلیل واریانس

تحلیل واریانس روشی است که بر اساس آن کل تغییرات یا پراکندگی موجود در مجموعه ای از داده ها به مولفه های گوناگون تقسیم می شوند. برای هر یک از این مولفه ها منبعی از پراکندگی وجود دارد. در این روش واریانس کل یا تغییرات کل به دو منبع یا دو مولفه واریانس بین گروه ها که نشان دهنده تفاوت های بین گروه ها است و منبع یا مولفه واریانس درون گروه ها که واریانس خطا نیز نامیده می شود و فرض می شود که ناشی از عوامل شانس یا تصادفی است، تقسیم می شود. به عنوان مثال اگر تاثیر سه روش تدریس A، B و C بر پیشرفت تحصیلی دانش آموزان در درس ریاضی مورد بررسی قرار گیرد، پس از اجرای این سه روش تدریس متفاوت، در سه نمونه از دانش آموزان سه میانگین پیشرفت تحصیلی در سه نمونه ( برای مثال سه میانگین ۱۷، ۱۶ و ۱۶/۵ ) به دست می آید. حال سوال پژوهشگر آن است که تفاوت بین این سه میانگین چگونه تفاوتی است؟ آیا ناشی از پراکندگی و تغییر بین خود افراد در درون گروه هاست و یا نه این تفاوت به عوامل فردی، خطا و شانس مربوط نمی شود بلکه مربوط به تفاوت بین گروه ها است که می تواند بیانگر تاثیر نوع روش های تدریس متفاوت در این سه گروه باشد. به عبارت دیگر اگر واریانس یا پراکندگی کل را با V_1 و واریانس یا پراکندگی بین گروه ها را با V_b و واریانس یا پراکندگی درون گروه ها و خطا را با V_e نشان دهیم فرمول ریاضی زیر را خواهیم داشت:

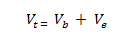این فرمول بیانگر آن است که ما می توانیم واریانس یا تغییرات کلی V_1 که در نمره های کل افراد وجود دارد را به دو قسمت واریانس یا تغییرات بین گروه ها V_b و واریانس یا تغییرات درون گروهی خطا V_e تجزیه کنیم. پس اگر واریانس بین گروه ها یا تغییرات بین گروه ها بیشتر باشد، انتظار می رود که واریانس درون گروه ها یا تغییرات درون گروه ها که ناشی از تفاوت های غیر واقعی یا تصادفی و ناشی از خطا است کمتر شود. برای فهم مفهوم تجزیه و تحیلیل واریانس به این مثال توجه کنید: اگر در مقایسه ای سه گروه با سه میانگین، واریانس که یا پراکندگی کل یا تغییرات کل مشاهده شده در نمرات V_t برابر ۱۰ و واریانس بین گروه ها که همان پراکندگی یا تغییرات بین گروه ها V_b است ۷ باشد، بنابراین واریانس درون گروه ها و یا واریانس خطا که همان پراکندگی یا تغییرات درون گروه ها V_e است ۳ خواهد بود. برای محاسبه واریانس انحراف هر نمره از میانگین محاسبه شده و مجذور می شود.  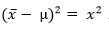سپس مجموع مجذورات انحرافات از میانگین همه نمره ها به دست می آید.

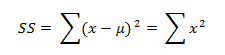برای محاسبه واریانس متغییر در جامعه، مجموع مجذورات انحرافات از میانگین به تعداد افراد جامعه و برای برآورد واریانس متغییر در جامعه از روی نمونه، بر ۱ – n تقسیم می شود.

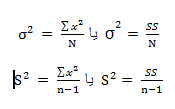با توجه به آنچه که گفته شد میتوان از رابطه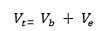رابطهرا نتیجه گرفت.

همان طور که در فرمول بالا ملاحظه می کنید هر چه که SS_w یعنی مجموع مجذورات انحراف از میانگین درون گروهی که بیانگر واریانس یا تغییرات ناشی از خطا و تفاوت های فردی است بیشتر باشد، SS_b یعنی مجموع مجذورات انحراف از میانگین بین گروه ها که بیانگیر واریانس یا تغییرات ناشی از تفاوت بین گروه ها است کمتر می شود. برای روشن شدن این رابطه در مثال مقایسه سه روش تدریس مجموع مجذورات انحراف از میانگین، SS_t یعنی همان واریانس یا پراکندگی یا تغییرات کل نمرات در درس ریاضی ۱۰۰ و مجموع مجذورات انحرافات از میانگین بین گروه ها SS_b یعنی همان واریانس یا پراکندگی یا تغییرات بین گروهی برابر ۷۵ در نظر می گیریم در نتیجه مجموع مجذورات انحرافات از میانگین درون گروه ها SS_w یعنی همان واریانس یا پراکندگی یا تغییرات درون گروهی ناشی از خطا و تفاوت های فردی ۲۵ خواهد بود. حال اگر پراکندگی بین گروهی ۳۰ بود، پراکندگی درون گروه که بیانگر تغییرات یا پراکندگی ناشی از خطا و عوامل تصادفی است، زیاد تر می شد: 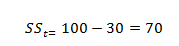با توجه به رابطه بالا هر چه تفاوت بین گروه ها زیادتر باشد، می توان گفت که تاثی متغییر مستقل بیشتر بوده است. در مثال ذکر شده نمره درس ریاضی، متغییر وابسته و سه روش تدریس که در سه گروه به طور جداگانه استفاده شدند، متغییر مستقل فرض شده اند. بنابراین زمانی که تغییرات بین گروه ها نسبت به تفاوت درون گروه ها سهم زیاد تری را در کل تغییرات به خود اختصاص داده باشد، بیانگر تاثیر بیشتر متغییر مستقل در متغییر وابسته است. همان طوری که شما محاسبه کردید، مجموع مجذورات انحرافات از میانگین بین گروهی در نمرات که ناشی از تفاوت های بین گروه ها بوده است، در این پژوهش زیاد ۸۰ است. لذا در این پژوهش تاثیر متغییر مستقل که همان شیوه فرزند پروری والدین می باشد، در رشد اجتماعی فرزندان قابل توجه است. برای این که پژوهشگر بتواند تصمیم بگیرد که آیا این تاثیر، تاثیر معنی داری بوده است یا نه، از مشخصه آماری F استفاده می کند. به عبارت دیگر مشخصه آماری F نسبت واریانس بین گروه به واریانس درون گروه ها را نشان می دهد. هر چقدر این نسبت بیشتر باشد، واریانس بین گروهی در مقایسه با واریانس درون گروهی بیشتر خواهد بود و در نتیجه میانگین بین گروه ها تفاوت بیشتری خواهد داشت. این نسبت معمولا به صورت زیر نوشته می شود: 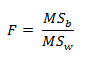میانگین مجذورات انحرافات از میانگین بین گروهی واریانس بین گروهی برآورد شده: میانگین مجذورات انحرافات از میانگین درون گروهی واریانس درون گروهی برآورد شده: هدف از بیان رابطه بین واریانس بین گروهی، واریانس درون گروهی و نسبت F، توضیح مفهوم تجزیه و تحلیل واریانس است. روش تجزیه و تحلیل واریانس انواع مختلفی دارد که ساده ترین نوع آن تجزیه و تحلیل واریانس یک طرفه است که در ادامه در این قسمت چگونگی محاسبه آن را در مراحل مختلف با ذکر مثال توضیح داده می شود. گام های شش گانه مربوط ه استفاده از آزمون معنی دار F برای مقایسه چند میانگین از چند جامعه مستقل برای محاسبه آزمون تجزیه و تحلیل واریانس یک راهه همانند سایر آزمون ها باید گام های شش گانه طی شود. لذا در این جا قبل از ذکر مثال به طور مختصر این مراحل ذکر می شود سپس همراه با مثال توضیح داده می شوند. گام اول: فرض صفر و فرض خلاف نوشته شود. در تحلیل واریانس یک راهه فرض صفر مطرح می کند که همه میانگین های جامعه های مستقل با هم مساوی هستند فرض صفر به این شکل نوشته می شود: 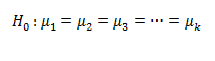فرض خلاف مطرح می کند که میانگین های جامعه ها با هم تفاوت معنی دار دارند. گام دوم: محاسبه نسبت F مشاهده شده با استفاده از رابطه 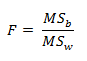است. گام سوم: محاسبه درجه آزادی. گام چهارم: تعیین سطح معنی داری که در این سطح فرض صفر آزمون می شود. گام پنجم: پیدا کردن F بحرانی جدول با توجه به محل تلاقی درجه آزادی صورت و درجه آزادی مخرج در سطح معنی داری مورد نظر. گام ششم: تصمیم گیری در مورد تایید یا رد فرض صفر اگر F محاسبه شده از F بحرانی جدول زیاد تر یا مساوی آن باشد، تصمیم به رد فرض صفر گرفته می شود.

مفروضه های تحلیل واریانس

برای استفاده از تحلیل واریانس و توزیع F برای آزمون فرض مربوط به مقایسه بیش از دو میانگین باید مفروضه های زیر برقرار باشد: نمونه ها به صورت تصادفی و مستقل از یکدیگر انتخاب شده باشند. اگر برای نمایش گروه های نمونه از حروف A، B، C و … استفاده کنیم در این صورت n_a معرف تعداد آزمودنی هایی است که در گروه نمونه A قرار دارند و n_B معرف تعداد آزمودنی هایی است که در گروه نمونه B قرار دارند و البته لزومی ندارد که گروه های نمونه حجم برابر داشته باشد، تنها شرط لازم این است که همه مشاهده ها هم داخل گروه و هم برای تمام گروه های نمونه، مستقل از یکدیگر باشند، مقصود آن است که انتخاب یک آزمودنی یا مشاهده معین از یک جامعه تاثیری در شانس انتخاب هیچ آزمودنی دیگر چه داخل آن جامعه و چه داخل یک جامعه دیگر نداشته باشد. همچنین نمره هر فرد مستقل ازنمره افراد دیگر باشد. اگر غیر از این باشد یعنی نمونه ها تصادفی یا مستقل از هم نباشند نمی توان از آزمون تحلیل واریانس استفاده کرد. به عنوان مثال در مقایسه سه شیوه ارزیابی متفاوت بر روی گروه ثابتی از دانش آموزان امکان استفاده از تحلیل واریانس یک راهه وجود ندارد زیرا در این جا سه میانگین از سه شیوه ارزیابی وجود دارد ولی به دلیل این که دانش آموزان مورد بررسی در سه شیوه ارزیابی مستقل از یکدیگر نبودند بلکه این سه شیوه ارزیابی در سه زمان مختلف بر روی گروه ثابتی از دانش آموزان انجام شده است، نمی توان از آزمون تحیلی واریانس یک راهه برای آزمون فرض این مثال استفاده کرد. فرض بر این است که جامعه هایی که از آنها نمونه های مورد مطالعه انتخاب شده است از لحاظ متقییر مورد مطالعه دارای توزیع نرمال باشد. به عنوان مثال اگر فرض پژوهش بررسی تاثیر نوع روش تدریس بر پیشرفت تحصیلی است، مدارسی که از جامعه مورد پژوهش بررسی تاثیر نوع روش تدریس بر پیشرفت تحصیلی دارای توزیع نرمال باشند. میزان پیشرفت تحصیلی دانش آموزان آن مدارس از نظر فراوانی از توزیع نرمال پیروی می کند و مطابق توزیع نرمال درهمه سطوح بالا، متوسط و ضعیف دانش آموز داشته باشند. بنابراین نمی توان گروه مورد مطالعه خود را از مدارس خاص که دانش آموزان ویژه ای دارند، انتخاب کرد زیرا در چنین مجموعه هایی دانش آموزان از نظر پیشرفت تحصیلی توزیع نرمال ندارند. واریانس ها یا تغییر پذیری نمره ها در جامعه هایی که نمونه ها از آنها انتخاب می شود مساوی باشند. برای رعایت این مفروضه باید واریانس هر یک از گروه های مورد مقایسه محاسبه شود و سپس تفاوت بین بزرگ ترین واریانس و کوچک ترین به دست آید و اگر این تفاوت چشمگیر نباشد از تحیل واریانس یک راهه استفاده گردد. البته قابل ذکر است که در صورت برابر بودن یا نزدیک بودن تعداد افراد گروه ها به یکدیگر میتوان از این مفروضه چشم پوشی کرد. متغییرهای مورد بررسی حداقل در سطح سنجش فاصله ای یا نسبتی باشند.

روش های مقایسه میانگین ها در تحلیل واریانس

آزمون تحلیل واریانس یک راهه، معنی داری تفاوت میانگین ها را آزمون می کند. اما در مورد این که میانگین چه گروهی بیشتر یا کمتر از گروه دیگر است، کارایی ندارد. به عبارت دیگر اگر نسبت F معنی دار باشد بیانگر آن است که پیشامدی رخ داده است و یا متغییر مستقل بر متغییر وابسته تاثیر گذاشته است ولی آزمون F مشخص نمی کند که کدام دو میانگین با هم تفاوت معین دار دارند. به عنوان مثال در مطالعه روش درمانی، نتیجه آزمون F نشان داد که تاثیر نوع روش درمانی برکاهش میزان اضطراب معنی دار است ولی چند سوال دیگر بدون پاسخ باقی می ماند: آیا میانگین گروه با روش درمانی A از نظر آماری از میانگین گروه با روش درمانی B کمتر است؟ آیا میانگین گروه با روش درمانی B از نظر آماری از میانگین گروه با روش درمانی C کمتر است؟ آیا بین میانگین گروه با روش درمانی A با معدل دو میانگین با روش درمانی B و C تفاوت معنی دار وجود دارد؟ برای پاسخگویی به چنین سوالاتی به روش آماری دیگری نیاز داریم. برای تحلیل و بررسی عمیق تر داده ها دو روش مقایسه وجود دارد که در مقایسه با آنچه تحلیل واریانس معمولی به دست می دهد، اطلاعات مفصل تری ارائه می دهد. هدف اصلی هر دو روش، مقایسه میانگین ها یا گروهی از میانگین ها است اما طرح ریزی آنها با یکدیگر تفاوت دارد. نخستین روش، تکنیک مقایسه های طرح ریزی شده یا قبل از تجربه یا پیشین خوانده می شود. دومین روش، تکنیک مقایسه های بعد از تجربه یا پسین Post hoc نامیده می شود.

مقایسه های طرح ریزی شده یا پیشین

در تکنیک مقایسه های طرح ریزی شده یا قبل از تجربه پژوهشگر به جای طرح ریزی برای تعیین این مطلب که آیا اثرهای آزمایشی یا تاثیر متغییر مستقل به طور کلی وجود دارد یا نه.در ابتدای کار قبل از تحلیل داده ها پرسش های خاصی را که مایل است در ارتباط با مقایسه میانگین ها بر اساس نظریه ها و تئوری های موجود جواب دهد مطرح می کند. به عنوان مثال پژوهشگری بر اساس نظریه ها و پژوهش های قبلی به این نتیجه رسیده است که مدت زمان مطالعه بر روی میزان یادگیری دانش آموزان تاثیری دارد. این پژوهشگر با توجه به یافته ها و تئوری های قبلی فرضیه خود را به این شکل تدوین می کند. زمان مطالعه بیشتر از ۴۵ دقیقه و کمتر از ۴۵ دقیقه میزان خطای زیادتری را در یادگیری ایجاد می کند. در پژوهش وی ۴ گروه دانش آموز با میزان مطالعه متفاوت گروه اول ۱۰ دقیقه، گروه دوم ۲۰ دقیقه، گروه سوم ۴۵ دقیقه و گروه چهارم ۷۵ دقیقه وجود دارند. در این پـژوهش گروه سوم باید با گروه اول و دوم و چهارم مقایسه شوند. برای مقایسه میانگین های این ۴ گروه از مقایسه های طرح ریزی شده یا پیشین استفاده می شود. شما درست حدث زدید این مشاور پژوهشگر به دلیل داشتن شواهد قبلی می تواند از مقایسه های طرح ریزی شده یا پیشین استفاده کند. در این جا به علت حجم زیاد و پیچیده شدن مطالب مربوط به مقایسه های پیشین از ذکر چگونگی محاسبات آن خودداری می شود.

مقایسه های پس از تجربه یا پسین

تکنیک مقایسه های پس از تجربه تنها در موقعیت هایی به کار می رود که در آنها تحلیل واریانس اولیه و آزمون F معنا دار بودن کلی را نشان داده باشد. در مقایسه های پس از تجربه می توان هر زوج از میانگین ها و هر ترکیبی از آنها را به صورت یک مقایسه مورد آزمانیش قرار داد. هرچند در بیشتر موارد پژوهشگر ممکن است علاقمند به مقایسه دو به دو میانگین ها باشد اما این روش ها را می توان برای آزمون هر نوع مقایسه به کار برد. برای آزمون معنا دار بودن مقایسه های پس از تجربه روش های زیادی وجود دارد از جمله روش کمترین تفاوت معنا دار LSD، آزمون t دانت ، نیومن- کولز ، توکی و شفه . از مفید ترین روش های چند مقایسه ای، دو روشی است که توکی و شفه ارائه داده اند که روش T و روش S خواند می شوند. در این جا چگونگی محاسبه و کاربرد این دو روش به طور مختصر توضیح داده می شود.

روش T یا توکی

اگر فرض صفر یعنی تساوی بین میانگین ها توسط یک تحلیل واریانس در سطح a رد شود برای آزمون تفاوت دو به دو میانگین از آزمون توکی می توان استفاده کرد. در روش توکی تعداد مقایسه های دو به دو میانگین ها از رابطه 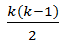 به دست می آید. مثلا اگر ۳ میانگین را بخواهیم دو به دو مقایسه کنیم، تعداد مقایسه ها به صورت زیر محاسبه خواهد شد: 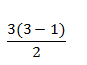در این جا چگونگی انجام آزمون توکی گروه ۱ با گروه ۲، گروه ۱ با گروه ۳ و گروه ۲ با گروه ۳ طی ۴ مرحله توضیح داده می شود. قبل از توضیح این مراحل باید برای انجام این آزمون سه مقدار داشته باشیم که این سه مقدار به صورت زیر به دست می آید:

تفاضل میانگین سه گروه به صورت دو به دو به دست می آید. مقدار بحرانی q که از جدول پیوست E کتاب استخراج می شود. مقدار q عبارت است از صدک هایی که با توجه به سطح معنی داری، تعداد گروه های مورد مقایسه و درجه آزادی مخرج درون گروهی که از رابطه N-K حاصل می شود، تعیین می گردد. برای مثال اگر سه گروه داشته باشیم که تعداد هر گروه ۱۰ نفر باشند و بخواهیم تفاوت معنی دار را در سطح a = 0/05 تعیین کنیم با مراجعه به جدول پیوست E کتاب مقدار بحرانی q را استخراج می کنیم که عبارت است از : همان طوری که در جدول پیوست E مشاهده می کنید صدک ۱۹۵ م در ستونی که بالای آن ۳ یعنی تعداد گروه نوشته شده است و ردیف آن ۲۴ می باشد به دلیل این که ردیف ۲۷ در جدول وجود ندارد و باید به درجه آزادی کوچک تر توجه شود. q بحرانی، ۳/۰۴۷ می باشد. خطای معیار آماره که با این فرمول محاسبه می شود: 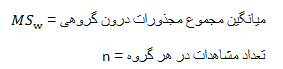به عنوان مثال اگر در پژوهشی که با استفاده از تجزیه و تحلیل واریانس مورد تحلیل قرار گرفته است میانگین مجموع مجذورات درون گروهی ۳ و تعداد هر گروه ۱۰ باشد خطای معیار آماره عبارت است از: 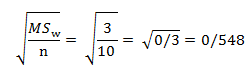چهار مرحله محاسبه آزمون توکی عبارت است از:

مرحله ۱- مقایسه های زوجی مشخص شود یا همان تعیین آماره. به عنوان مثال اگر سه عمل روش درمانی با هم مقایسه می شوند خواهیم داشت: 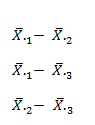مرحله ۲- تمام مقایسه های زوجی به خطای معیار آماره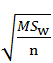تقسیم می شود بنابراین خواهیم داشت:

مرحله ۳- مقدار بحرانی q مربوط به این آزمون با استفاده از جدول E پیوست کتاب با توجه به درجه سطح معنی داری a، تعداد گروه و درجه آزادی درون گروهی تعیین می شود. بنابراین خواهیم داشت: 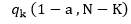مرحله ۴- جواب مرحله ۲ یعنی تقسیم آماره بر خطای معیار آماره با جواب مرحله ۳ یعنی مقدار بحرانی q که از جدول E پیوست کتاب استخراج شده است، مقایسه می شود. اگر جواب به دست آمده از مقدار q بیشتر باشد نتیجه گرفته می شود که دو میانگین دارای اختلاف معنی دار بوده اند و اگر جواب به دست امده از مقدار q کمتر باشد می توان نتیجه گرفت که تفاوت معنی داری بین دو میانگین وجود ندارد.

برای درک بهتر کاربرد آزمون توکی، چگونگی محاسبه این آزمون را در مثال پژوهشی مقایسه سه روش درمانی در کاهش اضطراب نشان می دهیم: همان طوری که به خاطر دارید در این مثال میزان اضطراب سه گروه ۵ نفره با سه روش درمانی A،B و Cمحاسبه شد و سه میانگین برای سه گروه به دست آمد که عبارت بودند از: 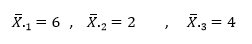در این مثال نتیجه تحلیل واریانس یک F معنی دار بود همچنین:

حال با استفاده از ۴ مرحله ارائه شده آزمون توکی مقایسه های دو به دو میانگین ها را در این مثال پژوهشی انجام می دهیم:

مرحله ۱- مشخص کردن تفاوت بین میانگین ها یا مقایسه های دو به دو، در این جا میانگین های سه گروه با سه روش درمانی به صورت دو به دو با هم مقایسه می شوند:

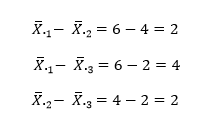مرحله ۲- تمام مقایسه های زوجی به خطای معیار آماره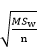تقسیم می شود.

مرحله ۳- استخراج مقدار q که مبنای مقایسه می باشد از جدول E که در پیوست ارائه شده است. جدول مزبور نشان می دهدکه مقدار q برای داده ها با ۰/۰۵=a و ۳= k و ۵=N-k برابر۳/۷۷است عبارت است از صدک ۹۵ام۳/۷۷

مرحله ۴- اگر قدر مطلق تفاوت میانگین ها که بر خطای معیار آماره تقسیم شده اند از مقدار بحرانی q تجاوز کند آن تفاوت معنی دار است. در این جا همان طوری که آماره ۳/۳ و همچنین مقایسه زوجی میانگین گروه دوم و سوم بعد از تقسیم بر خطای معیار آماره ۳/۳ بوده است که هر دو از مقدار بحرانی q 3/77 کمتر بودند پس تفاوت این میانگین ها تفاوت معنی داری نبوده است. در حالی که قدر مطلق تفاوت میانگین گروه اول با سوم که بر خطای معیار آماره تقسیم شده است ۶/۶ می باشد که از مقدار بحرانی q با ۰/۰۵ = a ، ۳ = k و df_w=12 بیشتر بوده است. بنابراین نتیجه گرفته می شود که میانگین گروه اول با روش درمانی A و گروه سوم با روش درمانی C دارای تفاوت معنی دار هستند.

روش شفه یا S

روش چند مقایسه ای شفه ۱۹۵۹ را می توان هم در مواردی به کار برد که از روش توکی T استفاده می شود و هم در مواردی که روش توکی قابل استفاده نیست. به عبارت دیگر در روش شفه علاوه بر این که می توان مقایسه دو به دو بین میانگین ها انجام داد مثل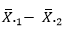مقایسه های دیگری هم قابل محاسبه است که به آنها مقابله گفته می شود به عنوان مثال اگر ۵ میانگین از میزان پیشرفت تحصیلی ۵ ناحیه از آموزش و پرورش شهر تهران را داشته باشیم علاوه بر مقایسه دو به دوی این میانیگین ها می توانیم مقابله های ترکیب دیگری نیز با استفاده از آزمون شفه انجام دهیم. برای مثال، مقایسه معدل میانگین ناحیه ۱، ۲ و ۳ با معدل میانگین ناحیه ۴ و ۵: برای انجام چنین مقابله ای لازم است به میانگین ها وزن یا ضریب داده شود. هر یک از میانگین ها یک ضریب و وزن می گیرند به طوری که جمع این ضریب ها صفر شود. در اینجا به علت پیچیده شدن مباحثات مربوط به مقابله های شفه از توضیح آن ها خودداری می شود.

علاوه بر این که روش شفه برای هر نوع مقایسه یا مقابله یا ترکیب های مختلف از میانگین ها قابل استفاده است، از این روش در رابه با پژوهش هایی که تعداد افراد آنها در گروه ها نابرابر می باشد می توان استفاده کرد. به عنوان مثال اگر در بیمارستانی میزان سلامت روانی پرستاران بخش های مختلف مورد مقایسه باشد به طوری که تعداد این پرستاران در هر بخش تفاوت قابل توجهی داشته باشد مقایسه های پسین روش شفه توصیه می شود. از ویژگی های دیگر آزمون شفه عدم حساسیت آن نسبت به نقض فرض های نرمال بودن و همگونی واریانس ها می باشد.