تابع گاما - Gamma Function
دسترسی سریع
مسئله یافتن تابعی که مقادیرش به ازای آرگومان های صحیح و مثبت فاکتوریل های ۱=!۱و۲=!۲ و ۶=!۳ و ... و 1.2.3...n!= n باشند توسط اویلر (Euler) به کمک انتگرال ناسره حل شد.
تابع گاما (کامل) 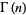 به صورت بسط فاکتوریل (factorial) به آرگومان های عددی مختلط و حقیقی است. این تابع با معادله ی زیر به فاکتوریل مرتبط می شود:
به صورت بسط فاکتوریل (factorial) به آرگومان های عددی مختلط و حقیقی است. این تابع با معادله ی زیر به فاکتوریل مرتبط می شود:
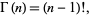
که این نماد مرسوم با توجه به گفتهی لژاندر به طور مختصری مشکلتر از نماد سادهتر معرفی شده توسط گائوس 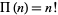 است (Gauss 1812; Edwards 2001, p. 8).
است (Gauss 1812; Edwards 2001, p. 8).
این تابع در همه جا به جز در ..., 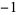 ,
, 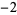
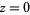 تحلیلی (analytic) است، و باقیمانده ی آن در
تحلیلی (analytic) است، و باقیمانده ی آن در 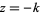 عبارت است از
عبارت است از
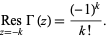
هیچ نقطه ی 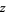 ای را نمی توان یافت که در آن
ای را نمی توان یافت که در آن 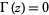 .
.
در استفاده ی مرسوم برای نمایش سری توانی از یک تابع گاما، یک قرارداد نمادگذاری وجود دارد. در حالیکه مولفانی همچون (Watson (1939 بر استفاده از 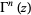 (یعنی بکارگیری از یک قرارداد تابع مثلثاتی-گون) تاکید دارند، طبق سنت نمادگذاری
(یعنی بکارگیری از یک قرارداد تابع مثلثاتی-گون) تاکید دارند، طبق سنت نمادگذاری ![[Gamma(z)]^n](http://mathworld.wolfram.com/images/equations/GammaFunction/Inline10.gif) استفاده می شود.
استفاده می شود.
تابع گاما را می توان به صورت یک انتگرال معین (definite integral) برای ![R[z]>0](http://mathworld.wolfram.com/images/equations/GammaFunction/Inline11.gif) تعریف کرد (شکل تعریف شده توسط اویلر)
تعریف کرد (شکل تعریف شده توسط اویلر)
(*) 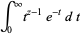
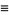
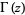
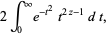
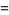
یا
![Gamma(z)=int_0^1[ln(1/t)]^(z-1)dt.](http://mathworld.wolfram.com/images/equations/GammaFunction/NumberedEquation3.gif)
تابع گامای کامل را می توان همچنین به تابع گامای ناتمام (incomplete gamma function) بالایی 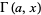 و تابع گامای ناتمام پایینی
و تابع گامای ناتمام پایینی 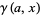 بسط داد.
بسط داد.
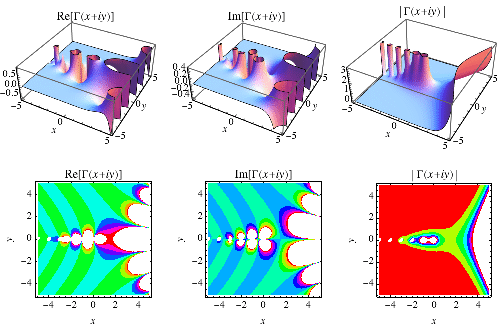
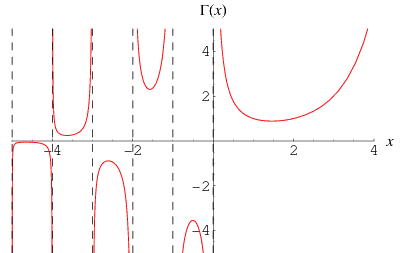
نمودار قسمت های حقیقی و موهومی 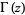 در صفحه ی مختلط در شکل بالا نشان داده شده است.
در صفحه ی مختلط در شکل بالا نشان داده شده است.
با انتگرال گیری جز به جز از معادله (*) برای یک آرگومان حقیقی، مشاهده می شود که
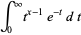
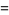
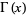
![[-t^(x-1)e^(-t)]_0^infty+int_0^infty(x-1)t^(x-2)e^(-t)dt](http://mathworld.wolfram.com/images/equations/GammaFunction/Inline27.gif)
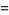
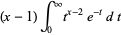
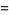
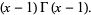
چنانچه  یک عدد صحیح باشد، آنگاه
یک عدد صحیح باشد، آنگاه
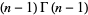
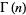
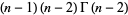
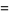
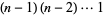
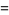
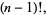
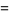
بنابراین تابع گاما به ازای آرگومان های صحیح مثبت (positive integer) به فاکتوریل تقلیل می یابد.
یک رابطه ی زیبا مابین 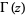 و تابع زتای ریمان (Riemann zeta function)
و تابع زتای ریمان (Riemann zeta function) 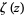 به صورت زیر است
به صورت زیر است
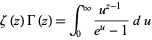
برای ![R[z]>1](http://mathworld.wolfram.com/images/equations/GammaFunction/Inline50.gif) (Havil 2003, p. 60).
(Havil 2003, p. 60).
تابع گاما همچنین می تواند به صورت یک حاصلضرب نامتناهی (infinite product) یعنی صورت ویراشتراوس (Weierstrass form) تعریف شود:
![Gamma(z)=[ze^(gammaz)product_(r=1)^infty(1+z/r)e^(-z/r)]^(-1),](http://mathworld.wolfram.com/images/equations/GammaFunction/NumberedEquation5.gif)
که 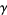 ثابت اویلر ـ ماشرونی (Euler-Mascheroni constant) است (Krantz 1999, p. 157; Havil 2003, p. 57). با لگاریتم گرفتن از طرفین معادله ی اخیر داریم:
ثابت اویلر ـ ماشرونی (Euler-Mascheroni constant) است (Krantz 1999, p. 157; Havil 2003, p. 57). با لگاریتم گرفتن از طرفین معادله ی اخیر داریم:
![-ln[Gamma(z)]=lnz+gammaz+sum_(n=1)^infty[ln(1+z/n)-z/n].](http://mathworld.wolfram.com/images/equations/GammaFunction/NumberedEquation6.gif)
با مشتق گیری از این رابطه بدست می آوریم:
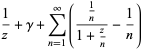
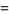
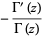
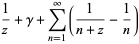
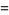
![-Gamma(z)[1/z+gamma+sum_(n=1)^(infty)(1/(n+z)-1/n)]](http://mathworld.wolfram.com/images/equations/GammaFunction/Inline60.gif)
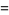
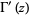
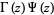
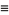
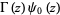
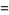
![-Gamma(1){1+gamma+[(1/2-1)+(1/3-1/2)+...+(1/(n+1)-1/n)+...]}](http://mathworld.wolfram.com/images/equations/GammaFunction/Inline69.gif)
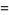
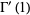
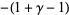
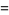
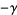
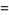
![-Gamma(n){1/n+gamma+[(1/(1+n)-1)+(1/(2+n)-1/2)+(1/(3+n)-1/3)+...]}](http://mathworld.wolfram.com/images/equations/GammaFunction/Inline78.gif)
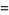
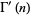
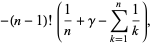
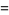
که 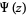 تابع دی گاما (digamma function) و
تابع دی گاما (digamma function) و 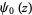 تابع چند گامایی (polygamma function) هستند.
تابع چند گامایی (polygamma function) هستند. 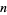 امین مشتق ها برحسب توابع چند گامایی (polygamma functions)
امین مشتق ها برحسب توابع چند گامایی (polygamma functions) 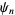 ,
, 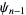 , ...,
, ..., 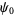 داده می شوند.
داده می شوند.
نظرات
هیچ نظری وجود ندارد.
افزودن نظر
مشاهده نقشه سایت
Copyright © 2017 - 2023 Khavarzadeh®. All rights reserved