تابع و توزیع دیریکله

1402/04/28

دسترسی سریع

یوهان پیتر گوستاو لوژن دیریکله متولد 1805 میلادی ریاضیدان آلمانی و معرفی کنندهٔ اصل کشوی دیریکله یا اصل لانه کبوتری می باشد.

تابع دیریکله

يكي از مباحث اساسي در رياضيات ، بررسي نقطه هاي پيوستگي وناپيوستگي توابع مي باشد. بررسی مفهوم روش حداکثر درست نمایی نیز در درک این موضوعات به شما کمک می کند. به عنوان مثال مجموعه ي نقطه هاي ناپيوستگي تابع براي عبارت است از مجموعه ي اعداد صحيح ( Z ) . و يا تابع f كه با ضابطه ي زير تعريف مي شود :

در هيچ نقطه اي پيوسته نيست و لذا مجموعه ي نقطه هاي ناپيوستگي آن ، R است . اين تابع به تابع ديريكله مشهور است . مطلبي كه در اين مقاله در پي آن هستيم ، معرفي تابعي است كه مجموعه ي نقطه هاي ناپيوستگي و پيوستگي آن به ترتيب : اعداد گويا و گنگ بازه ي باشند .

عکس های به کار برده شده در این مقاله متحرک میباشد ، برای مشاهده روی عکس ها کلیک نمایید.

تابع f را بر با ضابطه ي در نظر بگيريد . ادعا مي كنيم كه اين ، همان تابع مطلوب است.

اگر عدد گوياي دلخواهي در باشد ،عدد حقيقي را طوري مي گيريم كه باشد . اكنون براي دلخواه ، اگر y عدد گنگ دلخواهي در باشد ، آن گاه اما ، پس اين تابع در هيچ نقطه ي گويائي از پيوسته نيست .

با روشي مشابه اين تابع در 0=x ناپيوسته است . پس در تمام نقطه هاي گوياي ناپيوسته است .

حال اگر x عدد گنگ دلخواهي در و عدد حقيقي دلخواه باشد ، چون مجموعه ي متناهي است [چرا؟]پس براي مجموعه ي m هاي طبيعي كه متناهي است .اكنون قرار مي دهيم :

،به دليل گنگ بودن x داريم : .

حال اگر عدد گوياي دلخواهي باشد ، آن گاه [به تعريف اخير توجه كنيد]. و لذا .

اگر گنگ باشد آن گاه .

اين بحث نشان مي دهد كه مجموعه ي نقطه هاي ناپيوستگي و پيوستگي تابع مورد نظر به ترتيب عبارت اند از : اعداد گويا و اعداد گنگ بازه ي .

اكنون نمودار اين تابع را در زير مي آوريم : عکس های به کار برده شده در این مقاله متحرک میباشد ، برای مشاهده روی عکس ها کلیک نمایید.

به دليل شباهت نمودار اين تابع به شكل درخت كريسمس ، اين تابع را تابع درخت كريسمس گويند .

توزیع دیریکله

توزیع دریکله در نظریه احتمال و آمار یک توزیع پیوسته است. این توزیع بطور کلی حالت گسترش یافته توزیع بتا برای توابع چندمتغیره است. معمولا از توزیع دیریکله به عنوان توزیع پیشین در مدل سازی بیزی استفاده می شود؛ چرا که توزیع دیریکله مزدوج پیشین (conjugate prior) برای توزیع چندجمله ای و توزیع دسته ای (categotical) است. برای درک بهتر تابع گاما نیز می توانید مقالات مربوط به این موضوع را مطالعه کنید. تعمیم این توزیع فرایند دیریکله است.

تعریف ریاضی

تابع چگالی احتمال آن بصورت زیر است:

$f(x_1,\dots, x_{K-1}; \alpha_1,\dots, \alpha_K) = \frac{1}{\mathrm{B}(\alpha)} \prod_{i=1}^K x_i^{\alpha_i - 1}$

به ازای همه ی x₁, …, x_K–۱> ۰ بطوریکه x₁ + … + x_K–۱ < ۱, و x_K = 1 – x₁ – … – x_K–۱. چگالی در خارج از این ناحیه صفر است. ثابت نرمالیزاسیون به صورت زیر تعریف می شود:

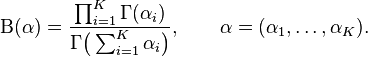
$\mathrm{B}(\alpha) = \frac{\prod_{i=1}^K \Gamma(\alpha_i)}{\Gamma\bigl(\sum_{i=1}^K \alpha_i\bigr)},\qquad\alpha=(\alpha_1,\dots,\alpha_K).$

حالت های خاص

یک حالت خاص زمانی است که تمامی مقادیر $\boldsymbol\alpha$ مقدار یکسانی داشته باشند، که در اینصورت آن را توزیع دیریکله ی متقارن می نامیم. در این حالت توزیع ساده می شود به:

$f(x_1,\dots, x_{K-1}; \alpha) = \frac{\Gamma(\alpha K)}{\Gamma(\alpha)^K} \prod_{i=1}^K x_i^{\alpha - 1}.$

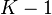زمانی که $\alpha=1$ توزیع معادل با توزیع یکنواخت روی یک تکیه‌گاه (ریاضی) سیمپلکس $K-1$ بعدی.

ویژگی ها

گشتاورها

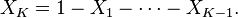فرض کنیم متغیرهای تصادفی $X = (X_1, \ldots, X_K)\sim\operatorname{Dir}(\alpha)$ و : $X_K=1-X_1-\cdots-X_{K-1}.$ را در اختیار داریم. تعریف می کنیم 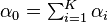$\textstyle\alpha_0 = \sum_{i=1}^K\alpha_i$ . بنابرین

$\mathrm{E}[X_i] = \frac{\alpha_i}{\alpha_0},$

$\mathrm{Var}[X_i] = \frac{\alpha_i (\alpha_0-\alpha_i)}{\alpha_0^2 (\alpha_0+1)}.$

علاوه بر این اگر if $i\neq j$

$\mathrm{Cov}[X_i,X_j] = \frac{- \alpha_i \alpha_j}{\alpha_0^2 (\alpha_0+1)}.$

مد

مد توزیع برداری مانند (x₁, …, x_K) است که در آن:

$x_i = \frac{\alpha_i - 1}{\alpha_0 - K}, \quad \alpha_i> 1.$

توزیع حاشیه ای

توزیع های حاشیه ای توزیع دیریکله، توزیع بتا هستند.

مزدوج برای توزیع چند جمله ای / دسته ای

این به این معنی است که اگر در مدلسازی مجموعه ای از داده ها از توزیع چندجمله ای/دسته ای استفاده کنیم و توزیع پیشین را دیریکله قرار دهیم، توزیع پسین الزاما یک توزیع دیریکله خواهد بود. به زبان ریاضی یعنی

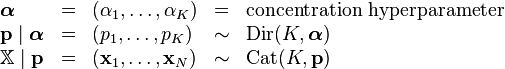
$\begin{array}{lclcl} \boldsymbol\alpha &=& (\alpha_1, \ldots, \alpha_K) &=& \text{concentration hyperparameter} \\ \mathbf{p}\mid\boldsymbol\alpha &=& (p_1, \ldots, p_K) &\sim& \operatorname{Dir}(K, \boldsymbol\alpha) \\ \mathbb{X}\mid\mathbf{p} &=& (\mathbf{x}_1, \ldots, \mathbf{x}_N) &\sim& \operatorname{Cat}(K,\mathbf{p}) \end{array}$

بنابرین روابط مقابل برقرار هستند:

$\begin{array}{lclcl} \mathbf{c} &=& (c_1, \ldots, c_K) &=& \text{number of occurrences of category }i \\ \mathbf{p} \mid \mathbb{X},\boldsymbol\alpha &\sim& \operatorname{Dir}(K,\mathbf{c}+\boldsymbol\alpha) &=& \operatorname{Dir}(K,c_1+\alpha_1,\ldots,c_K+\alpha_K) \end{array}$

ارتباط با توزیع دیریکله _ چندجمله ای آنتروپی

می دانیم

$\operatorname{E}[\log(X_i)] = \psi(\alpha_i)-\psi(\alpha_0)$

و

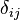$\operatorname{Cov}[\log(X_i),\log(X_j)] = \psi'(\alpha_i) \delta_{ij} - \psi'(\alpha_0)$

که در آن $\psi$ تابع دایگاما و $\psi'$ تابع ترایگاما، $\delta_{ij}$ دلتای کرونکر است.

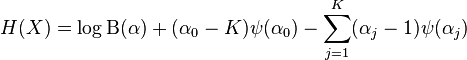
$H(X) = \log \mathrm{B}(\alpha) + (\alpha_0-K)\psi(\alpha_0) - \sum_{j=1}^K (\alpha_j-1)\psi(\alpha_j)$

تابع دایگاما برابر با مشتق لگاریتم تابع گاما می‌باشد، یعنی:

$\psi(x) =\frac{d}{dx} \ln{\Gamma(x)}= \frac{\Gamma'(x)}{\Gamma(x)}.$

تابع دلتای کرونکر (به انگلیسی: Kronecker delta)‏ تابعی با دو متغیر نامگذاری شده به نام ریاضیدان آلمانی لئوپولد کرونکر، و به صورت زیر تعریف می‌شود:

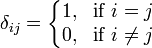
$\delta_{ij} = \left\{\begin{matrix} 1, & \mbox{if } i=j \\ 0, & \mbox{if } i \ne j \end{matrix}\right.$

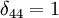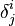بدین معنی که اگر دو متغیر با هم برابر بودند مقدار دلتا ۱، و در غیر این صورت مقدار آن صفر خواهد بود. به عنوان مثال $\delta_{23} = 0$ است و مقدار $\delta_{44} = 1$ خواهد بود. گاهی در جبر خطی و در حساب تانسور‌ها دو متغیر را به صورت مختصه بالا و پائین نمایش می‌دهند: $\delta^i_j$ .

این تابع در جبر خطی و بخصوص حساب تانسور‌ها و ماتریس‌ها کاربردهای فراوانی دارد و به ساده سازی محاسبات کمک شایانی می‌کند.

نظرات

هیچ نظری وجود ندارد.

تابع و توزیع دیریکله

دسترسی سریع

نظرات

افزودن نظر

آخرین مقالات