آزمون وایت

1402/06/14

دسترسی سریع

یکی از موضوعات مهمّی که در اقتصاد سنجی به آن برخورد می‌کنیم موضوع واریانس ناهمسانی است. واریانس نا همسانی به این معناست که در تخمین مدل رگرسیون مقادیر جملات خطا دارای واریانسهای نابرابر هستند. در واقع ما در تخمین رگرسیون که با استفاده از روش حداقل مربعات معمولی انجام می‌شود ابتدا فرض می‌کنیم که تمامی جملات خطا دارای ‍‍واریانسهای برابر هستند وبعد از ان که مدل را تحمین زدیم سپس با استفاده از یک سری روش‌ها و تکنیک‌ها به بررسی این فرض می‌پردازیم و این که آیا واقعاً در مدل ما واریانس همسانی وجود ندارد؟ ولی در مورد کارهای عملی اقتصاد سنجی همواره دو مسئله برای محقق پیش می‌آید ۱)با توجه به آن که مقادیر جملات خطا در جامعهٔ اصلی قابل مشاهده نمی‌باشد چگونه می‌توان به وجودواریانس ناهمسانی در مدل پی برد؟ ۲)در عمل بسیار غیر محتمل است که دقیقاً تمامی واریانس‌های جملات خطا با یکدیگر برابر باشند و معمولاً واریانس‌ها مقداری با یکدیگر تفاوت دارند. بنابراین سوال طبیعی که اینجا مطرح می‌شود این است که آیا معیاری آماری وجود دارد که میزان نابرابری واریانس‌ها را اندازه گیری کند تا با استفاده ار آن بتوانیم بگوییم که اگر میزان نابرابری واریانس‌ها از مقداری بیشتر باشد مدل ما مشکل واریانس ناهمسانی دارد. برای پاسخگویی به سوال فوق باید گفت که اقتصاددانان از روش‌های گوناگونی استفاده می‌کنند که می‌توان برای مثال آزمون بروش پاگان و آزمون وایت و آزمون پارک را نام برد که البته یکی از پرکاربرترین روشها آزمون وایت است.

موارد استفاده از آزمون وایت

معمولاً هنگامی از آزمون وایت استفاده می‌شود که توزیع واریانس جملات خطا را ندانیم و حدسی نیز در مورد آن نداشته باشیم و بنابراین آزمون وایت کلی‌ترین حالت را در نظر می‌گیرد و نسبت به تشخیص واریانس ناهمسانی بسیار حساس است.

مراحل تست وایت

۱)ابتدا مدل اصلی را با فرض عدم واریانس ناهمسانی تخمین می‌زنیم (ما فرض کرده‌ایم که دو متغیر توضیحی داریم البته این به راحتی قابل تعمیم به حالت عمومی با k متغیر توضیحی نیز می‌باشد.).(تخمین۱)و آنگاه مقادیر پسماندها و مربع مقادیر پسماندها را محاسبه می‌کنیم.

$ y_i =\beta_0+\beta_1X_{1i}+\beta_2X_{2i}+ u_i\, $

۲) سپس یک رگرسیون جدید بدین صورت می نوسیم:(تخمین ۲)

$e_i^2 = \gamma_0+\gamma_1X_{1i}+\gamma_2X_{2i}+\gamma_3X_{1i}^2+\gamma_4X_{2i}^2+\gamma_5X_{1i}X_{2i}+v_i$

یعنی آن که مربع پسماندها را روی تک تک متغیرهای توضیحی، مربع متغیرهای توضیحی و نیز حاصل ضرب دو به دو متغیرها رگرسیون می‌زنیم. فایدهٔ این کار این است که تقریباً تمام حالت‌های ممکن واریانس ناهمسانی را در نظر گرفته‌ایم. البته ممکن است گفته شود که واریانس ناهسانی می‌تواند در اثر اشکال دیگری از روابط میان پسماندها مثل تابع درجه سوم یا رادیکالی یا لگاریتمی ایجاد شود که در آزمون وایت آورده نشده‌اند ولی در جواب باید گفت:

اولاً:سایر حالت‌های واریانس ناهمسانی شباهت زیادی به حات‌های در نظر گرفته شده در آزمون وایت دارند و بنابراین گویا در نظر گرفته شده‌اند. دوم آن که:اگر ما تعداد متغیرهای توضحیحی را در تخمین ۲بیش از اندازه زیاد کنیم دچار مشکل هم خطی در تخمین ۲ می‌شویم بنابرابن به دلیل هم خطی ممکن است که ضریب تعیین مدل بالا رود و بنابراین ما به غلط مدلی زا که دارای واریانس ناهمسانی نیست دارای واریانس نا همسانی بپنداریم.

۳) آزمون F را برای معنی دار بودن کل رگرسیون از طریق فرمول زیر محاسبه می‌کنیم:

$F=\frac{\left(\frac{\R^2}{k}\right)}{\left(\frac{1-\R^2}{n -k-1}\right)}$

البته می‌توانیم از آماره ی زیر که به آماره ی ال ام معروف است هم استفاده کنیم که در این صورت با توزیع کی دو با درجه آزادی۵ مقایسه می‌کنیم،: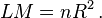 $ LM=nR^{2} \,. $

آماره ی F دارای توزیع فیشر با درجه آزادی ۵ و n-۵-۱، که در آن n تعداد مشاهدات می‌باشد. همچنین آماره LM دارای توزیع کی دو با ۵ درجه آزادی می‌باشد.

۴) مرحله قضاوت: اگر از آماره F استفاده کردیم آنگاه با درجه آزادی گفته شده مقایسه می‌کنیم و اگر از آماره LM استفاده کریم آنرا باتوزیع کی دو با درجه آزادی مربوطه مقایسه می‌کنیم، در این آزمون فرض صفر این است که واریانس همسانی داریم و بنابراین اگر آماره محاسبه شده از مقدار جدول بیشتر باشد در آنصورت مدل تصریح شده ابتدایی ما دارای واریانس ناهمسانی است.

روش دیگری برای آزمون وایت

در این روش به ترتیب مراحل زیر را انجام می‌دهیم: ۱)ابتدا مدل اصلی را با فرض عدم واریانس ناهمسانی تخمین می‌زنیم و آنگاه مقادیر پسماندها و مربع مقادیر پسماندها را محاسبه می‌کنیم. ۲)سپس با استفاده از پسماندهایی که به دست آورده‌ایم این بار یک رگرسیون جدید مینوسیم که مربع مقادیر پسماندها را به عنوان متغیر توضیحی و مقادیر تخمینی y و مربع مقادیر تخمینی y را به عنوان متغیر توضیحی در آن می‌آوریم. سپس این رگرسیون را تخمین می‌زنیم. ۳)برای تخمینی که به دست آورده‌ایم آماره اف یا ال ام را مثل حالت قبلی محاسبه می‌کنیم. ۴)اگر از آمارهٔ اف استفاده کرده‌ایم آن را با توزیع فیشر با درجه آزادی ۲ وn-۲-۱ مقایسه می‌کنیم و اگر از آمارهٔ ال ام استفاده کرده‌ایم آن را با توزیع چی دو با درجه آزادی ۲ مقایسه می‌کنیم. در این شیوه نیز مثل شیوهٔ قبل فرض صفر آن است که ما دارای واریانس ناهمسانی نمی‌باشیم و بنابراین اگر مقدار آمارهٔ آزمون از مقدار جدول بیشتر باشد در آن صورت مدل تصریح شدهٔ ابتدایی ما مشکل واریانس نا همسانی دارد. برای اطلاع از آزمون دو جمله ای نیز می توانید به مقالات تخصصی در این زمینه مراجعه کنید.

مقایسه دو روش آزمون وایت

همان طور که مشخص است نحوهٔ کلی و مراحل هر دو روش آزمون وایت یکسان است و تفاوت تنها در این است که در روش دوم به جای آن که مربع مقادبر پسماند را روی تک تک متغیرهای توضیحی و مربعاتشان و نیز حاصل ضربشان رگرسیون بزنیم روی مقادیر تخمینی متغیر وابسته و نیز مربع مقادیر تخمینی متغیر وابسته رگرسیون می‌زنیم و بنابراین با این کار باعث افزایش درجه آزادی مدل می‌شویم و در نتیجه در مرحلهٔ مقایسه نیز با توزیع اف یا توزیع کی دو با درجه آزادی کمتری مقایسه می‌کنیم.

نظرات

هیچ نظری وجود ندارد.