آزمون فیشر

آزمون فیشر (آزمون مقایسه داده های مستقل رده ای)

به منظور بررسی وابستگی میان دو گروه از داده های غیر زوجی، در صورتیکه داده های مورد نظر کیفی باشند از روش تحلیل جداول توافقی استفاده می شود. فرض صفر مورد آزمون در این حالت استقلال متغیرهای سطری و ستونی جدول و فرش مقابل وابستگی را بیان می کند. برای بررسی این فرضیات آزمون های مختلفی وجود دارد. آزمون فیشر از آن جمله است. همچنین خوب است نسبت به آزمون خی دو یا مجذور خی نیز اطلاعاتی بدست آورید.

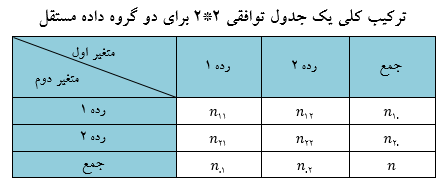
آزمون فیشر در حالت کلی برای هر تعداد از نمونه قابل استفاده است اما به طور خاص چنانچه حجم نمونه انتخابی کمتر از 10 باشد از این روش استفاده می شود. برای انجام این آزمون مقادیر فراوانی های مشاهده شده خانه های جدول و مقادیر فراوانی های مورد انتظار آن را به شرط برقراری فرض صفر محاسبه می کنیم. فراوانی های مورد انتظار خانه ij جدول (E_ij) از حاصلضرب جمع کناری سطر i ام در جمع کناری ستون j ام و تقسیم آن بر حجم کل نمونه (n) بدست می آید. یعنی :

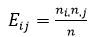
به این ترتیب مقدار آماره آزمون با استفاده از رابطه زیر حاصل می شود

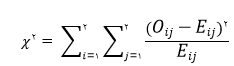
که در آن O_ij فراوانی مشاهده شده در خانه ij می باشد. اگر فرض صفر برقرار باشد آماره χ^2 از توزیع کای دو با 1 درجه آزادی پیروی می کند. بنابراین اگر آماره χ^2 در سطح معنی داری α بزرگتر از مقدار حاصل از جدول توزیع کای دو باشد، فرض صفر مبنی بر استقلال دو گروه پذیرفته نمی شود. نکته : توجه داشته باشید که این تقریب زمانی قابل اجرا است که E_ij≥5 برقرار باشد. چنانچه مقدار موجود در خانه های جدول کمتر از 5 باشد و یا به طور کلی حجم نمونه انتخابی کمتر از 10 مورد باشد، از مقدار آماره دقیق فیشر استفاده می شود. فیشر نشان داد که احتمال رخداد ترکیب تصادفی جدول 1 با استفاده از قانون احتمال فوق هندسی برابر است با :

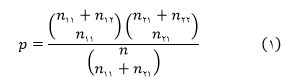
انجام آزمون فرض H_0: p_1=p_2 (که رد آن p_1 نسبت موفقیت ها در رده اول و p_2 نسبت موفقیت ها در رده دوم است)، معادل فرض مستقل بودن متغیرهای سطری و ستونی می باشد. برای آزمون این فرض در برابر فرض های مقابل ممکن ترکیب های دیگر جدول 2*2 را که فراتر از ترکیب مشاهده شده در در مسئله مورد بحث هستند پیدا می کنیم . احتمال های متناظر با ان ها را با فرض برقراری H_0 محاسبه می نماییم. از جمع بستن احتمال مشاهده شده این ترکیب ها با ترکیب ابتدایی جدول سطح معناداری کلی آزمون محاسبه می شود. منظور از «فراتر بودن» ترکیب، مشاده اعدادی در خانه های جدول است که تفاوت های بیشتری از شکل اولیه را در جهت تأیید فرض مقابل نشان دهند. مثال : 24 نوجوان به تصادف انتخاب شده و برحسب اینکه آیا رژیم غذایی خاصی را دنبال می کنند یا خیر به دو گروه تقسیم شده اند. فرض صفر مورد آزمون این است که جنسیت و داشتن رژیم غذایی از یکدیگر مستقل هستند. در برابر فرض مقابل کمتر بودن نسبت پسران دارای رژیم را بیان می کند. فرض های مورد آزمون را به صورت مقابل نیز می توان نوشت :

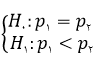
که در آن p_1 نسبت پسرانی است که رژیم غذایی دارند وp_2 نیز نسبت مشابه دختران را نشان می دهد.

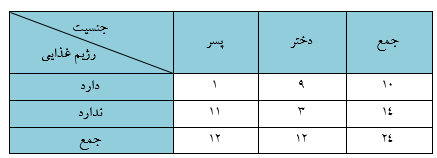
با استفاده از رابطه (1) سطح معناداری اولیه 0.0003 محاسبه می شود. ترکیب فراتر جدول فوق که به صورتی بهتر فرض مقابل یعنی کمتر بودن نسبت پسران دارای رژیم غذایی را تأیید می کند، به صورت جدول زیر است

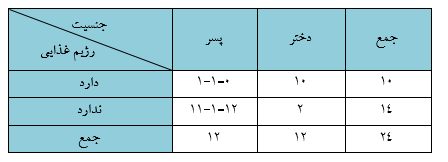
علت در نظر گرفتن این ترکیب از جدول آن است که فاصله بیشتر بین داده های دو رده (جنسیت یا رژیم غذایی) فرض مستقل بودن دو رده را بیشتر زیر سؤال می برد. به عبارت دیگر نزدیک شدن فراوانی رده های متغیرها و توزیع یکسان آن در رده های متغیر دیگر به معنای بی اثر بودن تغییرات یک متغیر بر دیگری است. با استفاده از جدول اخیر احتمال مورد نظر تقریبا برابر صفر حاصل می شود. و سطح معناداری کلی آزمون از جمع این دو مقدار برابر 0.0003 می باشد. اگر سطح خطای آزمون α=0.05 در نظر گرفته شود، فرض صفر مبنی بر استقلال متغیرهای رژیم غذایی و جنسیت، پذیرفته نمی شود.