آزمون علامت

آزمون علامت (آزمون آماری ناپارامتری مقایسه دو گروه وابسته)

در بسیاری از تحقیقات آزمایشی مایل به ارزیابی وضعیت یک متغیر در حالات متفاوت می با شیم. مانند ارزیابی میزان مسئولیت پذیری افراد قبل و بعد از یک دوره ی آموزشی. اینچنین نمونه هایی در آمار، نمونه های وابسته نامیده می شوند. حال این متغیر(مسئولیت پذیری) می تواند در دو یا چند وضعیت مورد ارزیابی قرار گیرد.بر این اساس آزمون های آماری ناپارامتری مربوط به نمونه های وابسته به دو دسته کلی تقسیم می شوند : آزمون های آماری مربوط به دو گروه وابسته و آزمون های آماری مربوط به چند گروه وابسته. آزمون هایی مانند آزمون علامت، آزمون ویلکاکسون و آزمون مک نمار برای مقایسه دو گروه وابسته مورد استفاده قرار می گیرند. همچنین لازم است تا با آزمون خی دو یا مجذور خی نیز آشنا شوید.

در این مطلب به معرفی آزمون علامت می پردازیم :

آزمون علامت مانند دیگر آزمون های ناپارامتری در مورد آزمون علامت نیز هیچ محدودیتی راجع به نوع توزیع متغیر مورد نظر وجود ندارد. اما مقادیر متغیر مورد نظر باید پیوستگی داشته و مقیاس آن از نوع ترتیبی باشد. بعبارت دیگر اجرای این آزمون برای متغیرهایی که دارای مقوله های محدودی هستند امکان پذیر نیست. در این آزمون نمره ی هر فرد در دو حالت در نظر گرفته می شود، اگر نمره ی اولیه فرد بیشتر از نمره فرد در وضعیت دوم باشد به آن نمونه علامت «-» داده می شود و در صورتی که نمره ی اولیه کمتر از نمره دوم باشد علامت «+» به آن نمونه اختصاص می یابد. در صورتیکه نمره فرد در دو وضعیت برابر باشد آن نمونه را از محاسبات آزمون حذف می نماییم.

به این ترتیب اگر تعداد علامت های مثبت و منفی برابر باشد، می توان نتیجه گرفت که گرایش مشخصی در افزایش یا کاهش نمره ها در دو وضعیت وجود ندارد. اما اگر تعداد مثبت ها بیشتر باشد به این معنی است که سطح نمرات در وضعیت دوم بهتر از وضعیت اول است و نهایتاً اگر نمرات منفی بیشتر باشد می توان بیشتر بودن نمرات در وضعیت اول را نتیجه گرفت.

برای مثال فرض کنید نمره اطلاعات عمومی افراد در دو وضعیت قبل و بعد از شرکت در یک دوره آموزشی اندازه گیری شده باشد. می خواهیم بدانیم آیا دوره آموزشی سطح اطلاعات عمومی افراد را افزایش داده است یا خیر؟

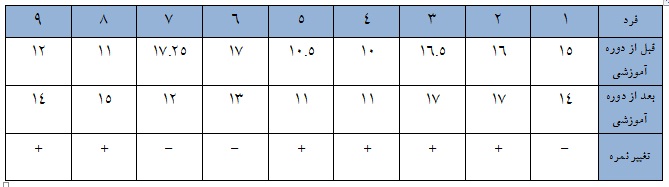
آماره ی آزمون معرفی شده برای بررسی مقایسه نمرات افراد در دو وضعیت به صورت زیر می باشد :

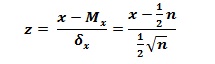
در این رابطه n تعداد کل افراد نمونه بوده و x فراوانی نشانه های مورد نظر محقق است (با توجه به فرضیه مورد آزمون). در صورتیکه حجم نمونه کم باشد از احتمال های تجمعی توزیع دو جمله ای برای قضاوت درباره آماره آزمون استفاده می شود. اما اگر حجم نمونه زیاد باشد تقریب توزیع نرمال برای این منظور کاربرد دارد.